9.1 Covarianza y Correlación

Una manera de medir qué tan relacionadas están dos variables aleatorias \(X\) y \(Y\) es considerando qué tan bien se puede aproximar una de ellas con otra mediante una función lineal. Es decir, podríamos considerar la nueva variable:

\[(Y - a - bX)^2\] y buscar \(a\) y \(b\) de manera que esta variable aleatoria tome los valores más chicos posibles.

Esta última frase tenemos que especificarla más. Podríamos por ejemplo buscar que su media sea lo más chica posible, es decir, resolver

\[\min_{a,b} E\left [ (Y - a - bX)^2 \right]\] usando que la suma de los valores esperados es igual al valor esperado de las sumas, y derivando e igualando a cero, podemos obtenemr que la mejor aproximación lineal a \(Y\) usando \(X\) está dada por

\[\mu_X + \rho \frac{\sigma_Y}{\sigma_X} (X - \mu_X)\] donde \(\mu_X\) y \(\sigma_X\) son media y desviación estándar de \(X\) y \(\mu_Y\) y \(\sigma_Y\) son media y desviación estándar de \(Y\), y la correlación \(\rho\) entre \(X\) y \(Y\) es \[\rho = \frac{E((Y-\mu_Y)(X-\mu_X))}{\sigma_X\sigma_Y}\] Nótese que esta cantidad no depende de la media ni de la escala de las variables \(X\) y \(Y\), pues centramos y dividimos entre la desviación estándar. El denominador de esta cantidad se llama covarianza entre \(X\) y \(Y\). Una cantidad muestral correspondiente a esta correlación es:

\[\hat{\rho} = \frac{\frac{1}{n}\sum (x_i - \bar{x})(y_i - \bar{y})}{\hat{\sigma_x}\hat{\sigma_y}}\] Por ejemplo:

propinas <- read_csv("./datos/propinas.csv")
#> 
#> ── Column specification ────────────────────────────────────────────────────────
#> cols(
#>   cuenta_total = col_double(),
#>   propina = col_double(),
#>   fumador = col_character(),
#>   dia = col_character(),
#>   momento = col_character(),
#>   num_personas = col_double()
#> )
cor(propinas$cuenta_total, propinas$propina)
#> [1] 0.6757341

que también podemos calcular como

x <- propinas$cuenta_total
y <- propinas$propina
media_x <- mean(x)
media_y <- mean(y)
sd_x <- sd(x)
sd_y <- sd(y)
mean((x - media_x)*(y - media_y)) / (sd_x * sd_y)
#> [1] 0.6729647

Nota: en R y muchos paquetes, en la fórmula de la correlación de arriba se divide entre \(n-1\) en lugar de \(n\) (lo cual no es importante a menos que \(n\) sea chica), y eso explica la diferencia entre los dos cálculos. La razón es en algunos casos al dividir entre \(n-1\) obtenemos un estimador de la correlacción que tiene propiedades que a veces son covenientes.

9.2 Discusión

Nótese que el término simétrico en la fórmula de la relación lineal entre \(X\) y \(Y\) que vimos arriba es la correlación \(\rho\). Los otros términos son simplemente centrados y escalamientos.

El valor de \(\rho\) siempre está entre -1 y 1, y decimos que la relación lineal es fuerte (positiva o negativa) cuando está cerca de estos valores. Cuando está cerca de cero, decimos que la relación lineal entre estas dos variables no es fuerte.

9.2.1 Ejemplo

library(corrplot)
#> corrplot 0.88 loaded
corrplot(cor(mtcars), method = "number")

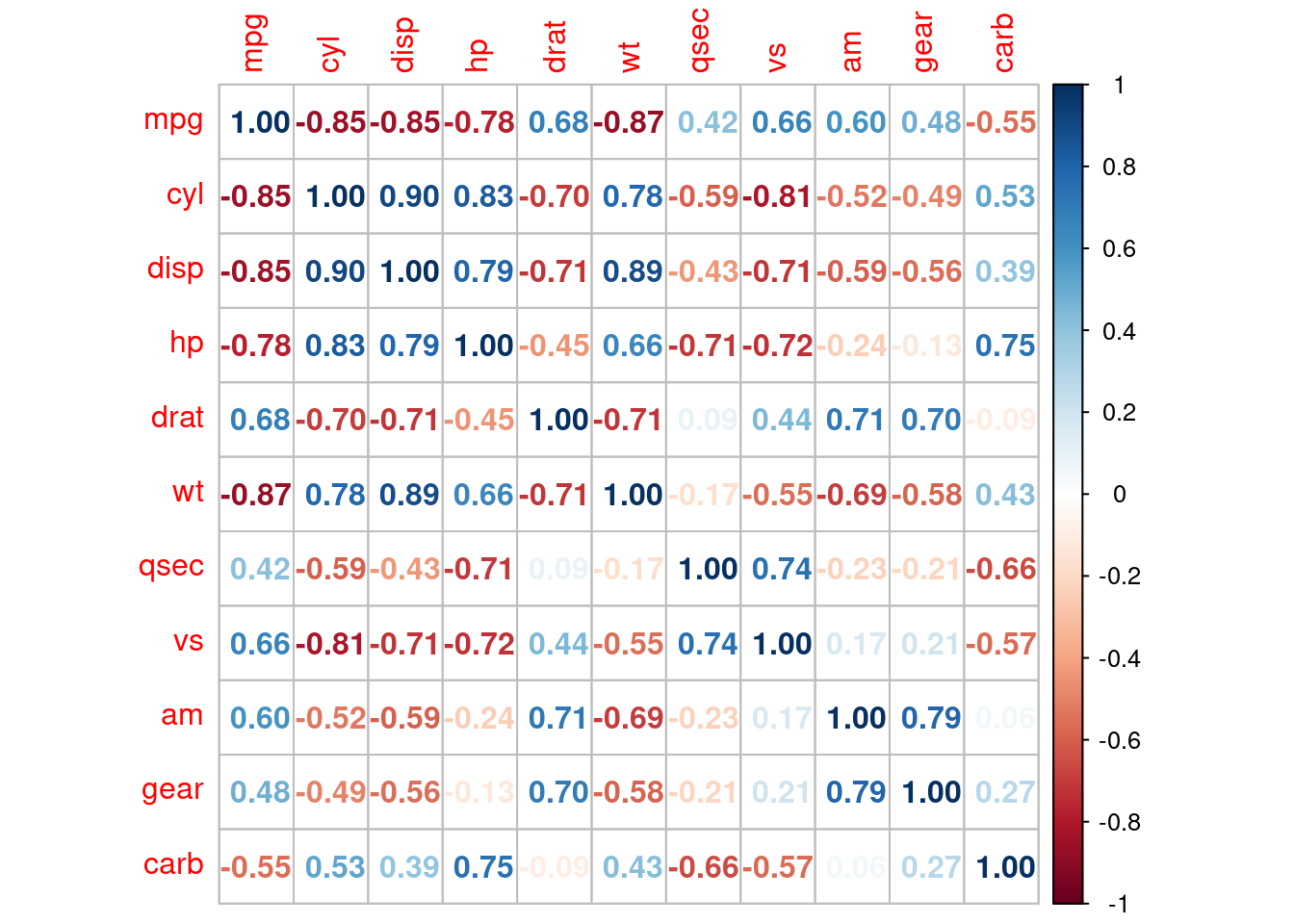- La matriz es simétrica. Leemos uno de los triángulos buscando primero las correlaciones más cercanas a 1 y más cercanas a -1. - Por ejemplo, la correlación de -0.85 entre peso de un coche y rendimiento (millas por galón, pero también podemos pensar en kilómetros por litro, ¿por qué?) indica una relación lineal fuerte y negativa entre estas variables: cuantos más peso tiene un coche, menos tiende a ser su rendimiento. - Aunque la interpretación depende del tamaño de muestra y del área específica de estudio, se consideran correlaciones fuertes como las que tienen valor absoluto mayor a 0.5. - Otro ejemplo: la variable gear (número de velocidades) no tiene una correlación lineal fuerte con qsec, por ejemplo.

Veamos dos gráficas:

ggplot(mtcars, aes(x = wt, y = mpg)) + geom_point()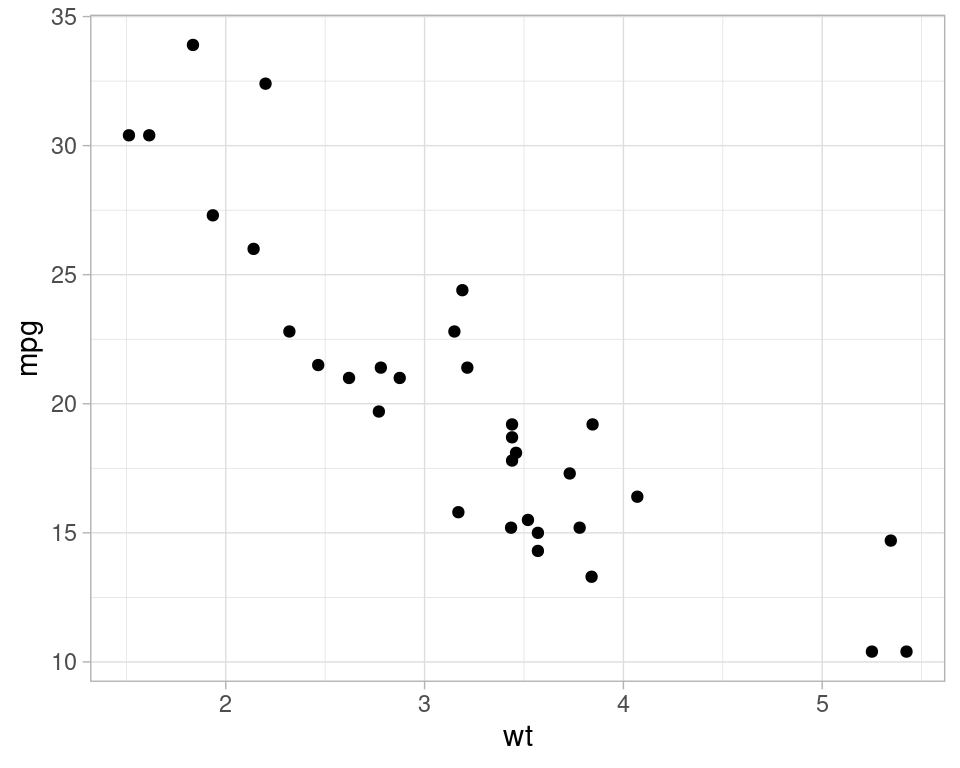

Y efectivamente vemos esta relación lineal clara, aunque modelar esta relación correctamente probablemente no debería de hacerse lineal (¿por qué?)

Por otro lado, para el par de variables con correlación baja:

mtcars <- mtcars %>% mutate(manual = factor(am))
ggplot(mtcars, aes(x = gear, y = hp, colour = manual)) + 
    geom_jitter(width = 0.1, height = 0)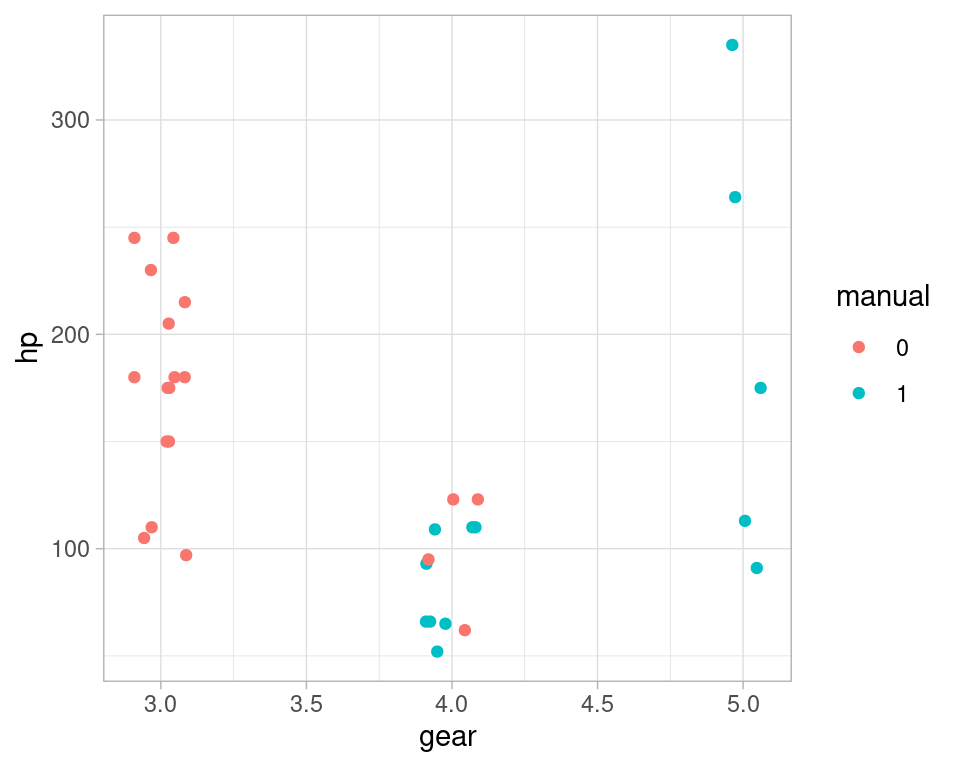

donde vemos que aunque no hay evidencia de correlación lineal, estas dos variables parecen tener relación. Esta relación, sin embargo, no es lineal, y la correlación aparece cercana a a 0.

En general, desventajas de usar la matriz de correlaciones como descriptivo para comenzar el análisis son:

• No capturan relaciones no lineales. En algunos casos pueden poner correlación 0 a variables que están fuertemente relacionadas.
• No son robustas a datos atípicos (igual que media y varianza)
• Son cantidades difíciles de explicar y entender.

9.3 Usando scores predictivos

En muchos casos, en lugar de usar relación lineal podemos usar medidas de qué tan bien puede predecirse una variable en términos de otra, no necesariamente de forma lineal.

Una idea us utilizar alguna implementación de un score de poder predictivo. Ver por ejemplo aquí.

#devtools::install_github('https://github.com/paulvanderlaken/ppsr')
library(ppsr)
pp_score <- score_df(mtcars,
                     n_cores = 8,  seed=232, do_parallel = TRUE)

pp_score %>% 
    filter(y == "gear") %>% 
    arrange(desc(pps)) %>% 
    head(10)
#>         x    y                       result_type        pps metric
#> 1    gear gear predictor and target are the same 1.00000000   <NA>
#> 2    drat gear            predictive power score 0.60718449    MAE
#> 3    disp gear            predictive power score 0.37286669    MAE
#> 4      am gear            predictive power score 0.35525992    MAE
#> 5  manual gear            predictive power score 0.35525992    MAE
#> 6     cyl gear            predictive power score 0.33278617    MAE
#> 7      hp gear            predictive power score 0.20268525    MAE
#> 8      wt gear            predictive power score 0.18619017    MAE
#> 9     mpg gear            predictive power score 0.14012843    MAE
#> 10     vs gear            predictive power score 0.05717949    MAE
#>    baseline_score model_score cv_folds seed algorithm model_type
#> 1              NA          NA       NA   NA      <NA>       <NA>
#> 2       0.6918974   0.2830067        5  232      tree regression
#> 3       0.6918974   0.4340149        5  232      tree regression
#> 4       0.6918974   0.4397184        5  232      tree regression
#> 5       0.6918974   0.4397184        5  232      tree regression
#> 6       0.6918974   0.4765879        5  232      tree regression
#> 7       0.6918974   0.5700230        5  232      tree regression
#> 8       0.6918974   0.5701773        5  232      tree regression
#> 9       0.6918974   0.6006758        5  232      tree regression
#> 10      0.6918974   0.6601575        5  232      tree regression

visualize_pps(mtcars, 
              do_parallel = TRUE, n_cores = 8, color_text = "gray20")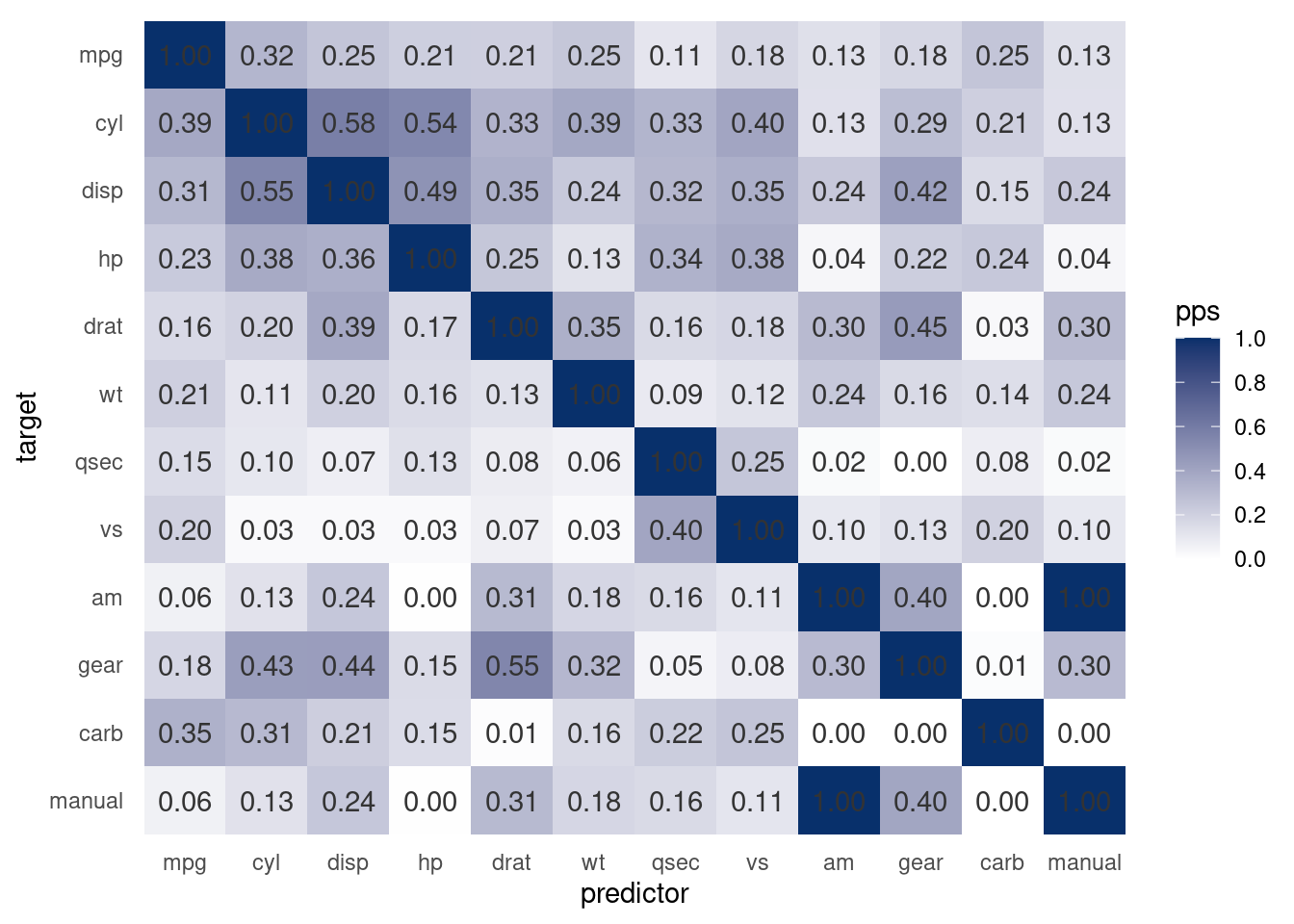

En este caso, predecir hp usando gear es alrededor de 20% mejor que no utilizar ninguna variable (haciendo predicciones con el modelo base). Estos cálculos se hacen con validación cruzada para sobreestimar la contribución de las variables.

• Estos scores son más fáciles de explicar, aunque son más complejos de calcular y requieren más cómputo.
• Son útiles porque pueden capturar relaciones no lineales, lo cuál ayuda en guiar el análisis.
• Pueden ser más robustos (dependiendo del modelo que se use para hacer las predicciones. En este caso se utilizan árboles de decisión).
• Sin embargo, no muestran la dirección de la relación
• Ver más en la liga mostrada arriba.