7 Modelos probabilísticos para variables continuas
En la parte anterior consideramos un númeroo fijo de resultados numéricos de experimentos aleatorios, por ejemplo, cuando \(X\) el resultado de una tirada de dado. En este caso, un modelo de probabilidad para \(X\) asigna una probabilidad dada a cada posible resultado, por ejemplo \[P(X=1) = 1/6\] e igualmente \(P(X=2)=\cdots = P(X=6) = 1/6\). En muchos casos, la cantidad \(X\) que nos interesa puede tomar valores numéricos arbitrarios, y en este esquema no está claro cómo asignaríamos probabilidades.
7.0.1 Ejemplo: ruleta justa
Supongamos que giramos una ruleta con una flecha indicadora, y el resultado del experimento es el ángulo en grados final de la flecha. ¿Cómo podríamos poner, por ejemplo \(P(X= 92.7)\)? ¿Qué pasa si podemos medir con resultados con varios decimales de exactitud?

Ruleta
En estos casos, en lugar de considerar eventos de la forma \(X=a\), podemos considerar eventos resultantes de la forma \(a\leq X \leq b\), es decir, buscamos asignar probabilidades a eventos de la forma \[P(X \in [a,b]).\] Por ejemplo, si \(Y\) es la estatura adulta de una persona que acaba de nacer, podríamos preguntarnos cómo asignar probabilidades a eventos como \[P(Y\in [150,170]) = P(150\leq Y \leq 170),\] y quizá también otros como \[P(Y < 180).\]
7.1 Modelo equiprobable o uniforme
Los modelos más simple para una medición continua \(X\) son los modelos uniforme.
Para nuestra ruleta, por ejemplo, \(X\) puede tomar valores en el intervalo \([0, 360)\). Si la ruleta es justa, entonces la probabilidad de que la flecha caiga en cualquier sector \([a,b]\) debe ser igual. Una manera de lograr esto usar como probabilidad la proporción de la longitud de \([a,b]\) con respecto al total de \([0, 360)\):
\(P(X\in [a,b]) = \frac{b-a}{360}.\)
- Discute por qué esta asignación de probabilidades satisface las tres reglas básicas de probabilidad (axiomas) que presentamos anteriormente.
- Este es el equivalente continuos para espacios equiprobables con un número finito de resultados.
Supongamos que una variable aleatoria puede tomar valores en el intervalo \([L,U]\). La variable aleatoria es uniforme en \([L,U]\) cuando
\[P(X \in [a,b]) = \frac{b-a}{L-U}\]7.1.1 Ejemplo: ruleta sesgada
Ahora supongamos que nuestra ruleta no está del todo balanceada. Por ejemplo, podría ser estuviera colgada en una pared, y al girar la flecha es un poco más probable que la flecha apunte hacia el piso en lugar de hacia el cielo.
En este caso, si la dirección hacia arriba es 90 grados y hacia abajo es 270 grados, quisiéramos por ejemplo que \[P(260 < X <280) < P(80 < X < 100)\] Y nótese que debe ser posible asignar probabilidades a cualquier sector de la ruleta con el nuevo modelo que propongamos. ¿Cómo podríamos modificar nuestra asignación de probabilidades?
Una de las maneras más fáciles es pensando que nuestra probabilidad se obtiene integrando una funcion constante:
- Si \([a,b]\) es un sector de la ruleta con \(a<b\), podríamos poner \[P(X\in [a,b]) = \int_a^b \frac{1}{360} \,dx = \frac{b-a}{360}\] De forma que si \(f(x)= 1/360\) para valores \(0 \leq x < 360\), nuestra probabilidad se escribe como la integral
\[P(X\in [a,b]) = \int_a^b f(x) \,dx \]
- En este caso, probabilidad es área bajo la curva \(f(x)=1/360\) que se calcula integrando sobre el intervalo de interés
Para generalizar la idea es la siguiente:
- Usamos la fórmula anterior, pero modificamos o perturbamos la función \(f(x) = 1/360\) para que \(f\) sea un poco más alta alrededor de 270 grados (abajo), y un poco más baja alrededor de 90 grados (arriba).
- Lo único que necesitamos es que \(f(x)\) no puede tomar valores negativos (por que si no obtendríamos probabilidades negativas en algunos sectores), y la integral sobre la ruleta completa debe ser uno:
\[P(X\in [0, 360]) = \int_0^{360} f(x)\,dx = 1\] Podríamos utilizar por ejemplo:
f_dens <- function(x){
x_rad <- 2 * pi * x / 360
(1/360) + 0.0002 * cos(x_rad - 3 * pi / 2)
}
graf_1_tbl <- tibble(angulo = seq(0, 360, 1), tipo = "uniforme",
f = 1 / 360)
graf_2_tbl <- tibble(angulo = seq(0, 360, 1), tipo = "colgada") %>%
mutate(f = f_dens(angulo))
graf_tbl <- bind_rows(graf_1_tbl, graf_2_tbl)
ggplot(graf_tbl, aes(x = angulo, y = f, colour = tipo)) +
geom_line() +
ylim(c(0, 0.003)) + facet_wrap(~tipo, nrow = 1) El cálculo se hace ahora con área bajo la curva. Para calcular
la probabilidad
\[P(X\in [50, 130]),\]
integramos la función \(f\) correspondiente, que corresponde a calcular
área bajo la curva:
El cálculo se hace ahora con área bajo la curva. Para calcular
la probabilidad
\[P(X\in [50, 130]),\]
integramos la función \(f\) correspondiente, que corresponde a calcular
área bajo la curva:
ggplot(graf_tbl, aes(x = angulo, y = f, colour = tipo)) +
geom_line() +
ylim(c(0, 0.003)) + facet_wrap(~tipo, nrow = 1) +
geom_area(aes(x = ifelse(angulo > 50 & angulo < 130, angulo, 0)),
fill="salmon", alpha = 0.5)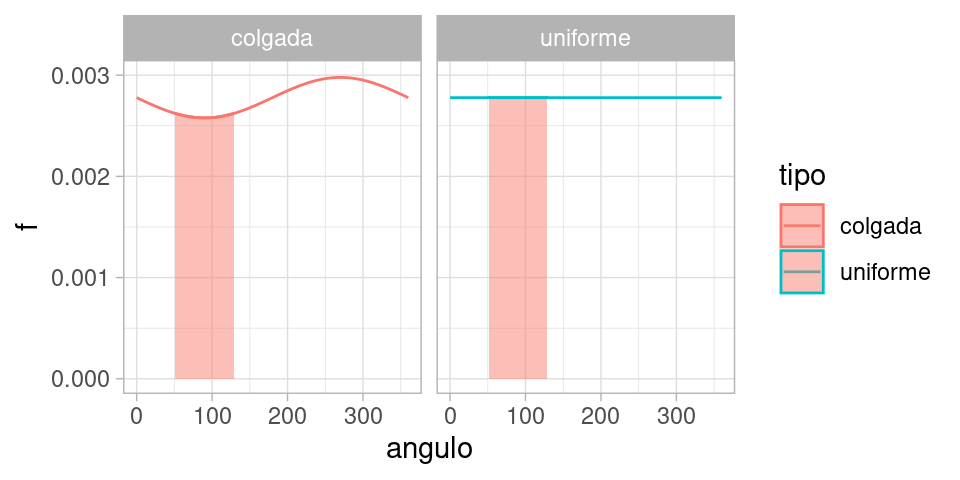
Y ahora vemos que para la versión perturbada, más de la probabilidad se concentra alrededor de 270 grados que alrededor de 90. Por las propiedades de la integral, todas las propiedades usuales de probabilidad se cumplen.
7.2 Funciones de densidad
Cuando trabajamos con mediciones de tipo continuo, es más conveniente definir asignaciones de probabilidad utilizando funciones de densidad de probabilidad:
Una función \(f(x)\) no negativa cuya integral es igual a 1 es una función de densidad de probabilidad. Las probabilidades asociadas se calculan integrando:
\[P(X\in [a,b]) = \int_a^b f(x)\,dx\]
En este caso decimos que \(f\) es la función de densidad de probabilidad asociada a la variable aleatoria \(X\). A este tipo de variables aleatorias les llamamos continuas.7.3 Ejemplo: densidad triangular
Supongamos que tenemos una variable aleatoria que tiene mediana 2, y puede tomar valores entre 0 y 4. Podríamos definir una densidad como sigue: Si \(x\) está entre 0 y 2, entonces
\[f(x) = \frac{x}{4}\] y si \(x\) está entre 2 y 4, entonces \[f(x) = 1 - \frac{x}{4}\]
dens_triangular <- function(x){
(x > 0) * (x < 4) * ifelse(x < 2, x/4, 1 - x/4)
}
triangular_tbl <- tibble(x = seq(-1, 5, 0.001)) %>%
mutate(f = dens_triangular(x))
ggplot(triangular_tbl, aes(x = x, y = f)) +
geom_line()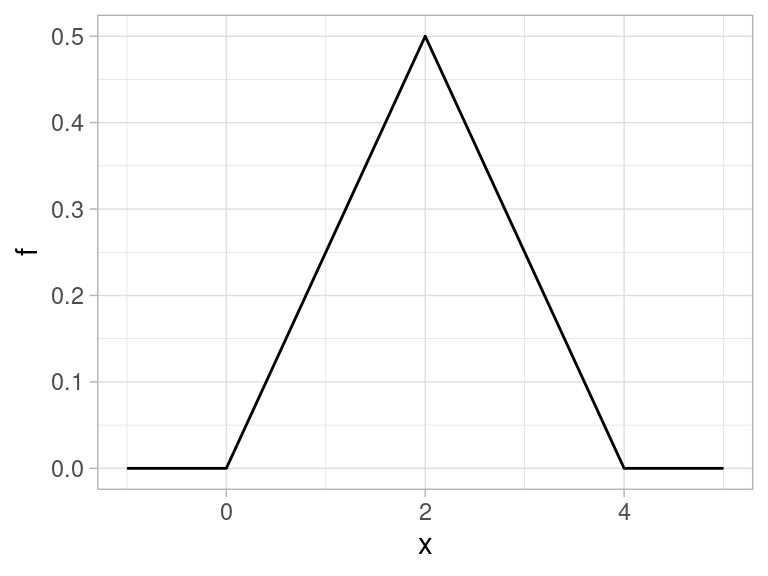
Ejemplo
Supongamos que una variable \(X\) tiene mediana 2 y rango de 0 a 4, con densidad triangular. ¿Cuál es la probabilidad \(P(X>1)\)?
Solución: Por reglas usuales de probabilidad, \(P(X>1) = P(1<X<2) + P(X\geq2)\). Tenemos que \(P(X\geq 2) = 0.5\). Ahora usamos la fórmula de la densidad triangular para obtener \[P(1<X<2) = \int_{1}^{2} f(x)\,dx = \int_1^2 \frac{x}{4}\,dx = \left [\frac{x^2}{8}\right ]_1^2 = 1/2 - 1/8 = 3/8 = 0.375\]
de modo que
\[P(X<1) = 0.375 +0.500 = 0.875\]
En general, podemos dar una fórmula para una densidad triangular en el intervalo \([A,B]\) con mediana en \((A + B)/2\). ¿Cómo sería la fórmula?
7.4 Cuantiles de variables aleatorias
Antes vimos la definición de cuantiles para datos numéricos. Podemos definirlos también para variables aleatorias numéricas:
Sea \(p\in (0,1)\). El cuantil-\(p\) de la variable \(X\) con función de densidad \(f(x)\) es el valor \(x(p)\) tal que
\[\int_{-\infty}^{x(p)} f(x)\,dx = p\]Observación: nótese que usamos como límite inferior \(-\infty\) para indicar que integramos \(f\) sobre toda la densidad que esté a la izquierda de \(x(p)\).
Ejemplo: densidad triangular
Supongamos que \(X\) tiene la densidad triangular mostrada arriba. Calcula el cuartil inferior y superior (es decir, los cuantiles 0.25 y 0.75). Para el cuartil superior, por ejemplo, buscamos al \(x(0.75)\) de la siguiente gráfica:
source("R/triangular.R")
ggplot(triangular_tbl, aes(x = x, y = f)) +
geom_line() +
geom_area(aes(x = ifelse(x > 0 & x < qtri(0.75, 0, 4), x, 0)),
fill="salmon", alpha = 0.5) +
ylim(c(0, 0.7)) +
annotate("text", x = qtri(0.75, 0, 4), y = 0.03, label = "x(0.75)") +
annotate("point", x = qtri(0.75, 0, 4), y = 0.0) 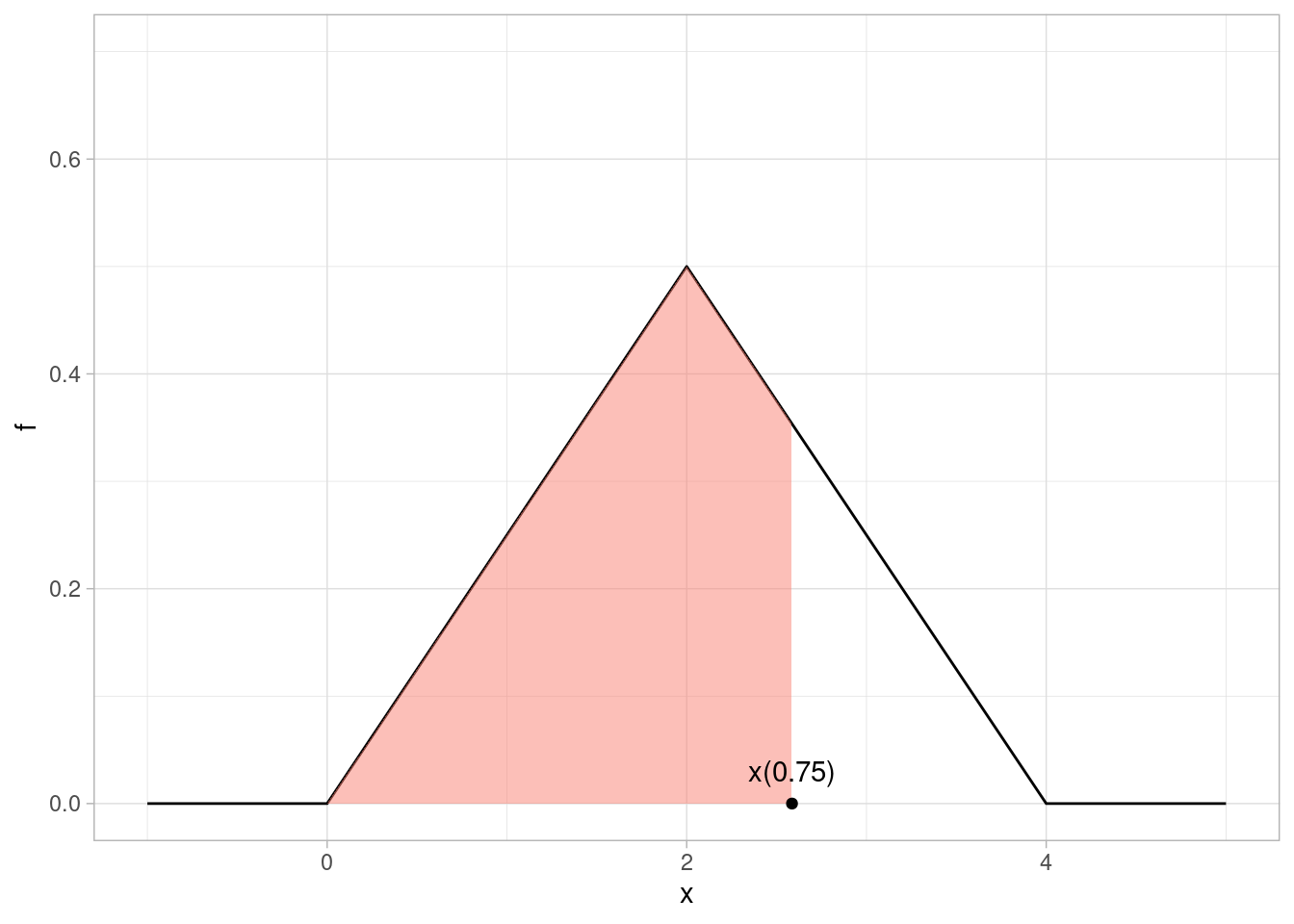
Comenzaremos por el cuartil inferior. Buscamos una \(x(0.25)\) tal que \[\int_0^{x(0.25)} f(x)\,dx = 0.25\] Sabemos que \(x(0.25)< 2\), pues la integral hasta 2 es 0.5, así que
\[\int_0^{x(0.25)} f(x)\,dx = \int_0^{x(0.25)} x/4 \,dx = \left [ x^2/8\right]_0^{x(0.25)} = (x(0.25))^2/8\] Si queremos que este valor sea igual a 0.25, entonces despejando obtenemos \[x(0.25) = \sqrt{0.25(8)} = \sqrt{2}\approx 1.4142\] Ahora podríamos calcular la otra integral, pero por simetría podemos concluir que \[x(0.75) = 2 + (2 - 1.4142) \approx 2.5858\] y concluimos que los cuartiles inferiores y superiores son aproximadamente 1.41 y 2.59
7.5 Comparando cuantiles teóricos y empíricos
Los cuantiles que vimos en la parte de descriptivos para datos numéricos se llaman usualmente cuantiles empíricos. Estos cuantiles podemos compararlos con cuantiles teóricos para ver qué tan similares son, y si el modelo teórico describe adecuadamente los datos.
7.5.1 Ejemplo: distribución uniforme
Simularemos 500 datos uniformes en \([0, 10]\):
x_sim_u <- runif(500, 0, 10)Podríamos calcular algunos cuantiles empíricos:
Por el ejercicio anterior sabemos cuáles son los cuantiles teóricos correspondientes a una uniforme en \([0,10]\). Podemos calcularlos también como sigue:
Y vemos que son muy similares los cuantiles empíricos y teóricos. Una mejor manera de considerar esta similitud es graficando todos los cuantiles empíricos y comparándolos con los teóricos:
ggplot(tibble(x = x_sim_u), aes(sample = x)) +
geom_abline(colour = "red") +
geom_qq(distribution = stats::qunif, dparams = list(min = 0, max = 10)) +
xlab("Cuantiles Teóricos U(0,10)") + ylab("Cuantiles de datos")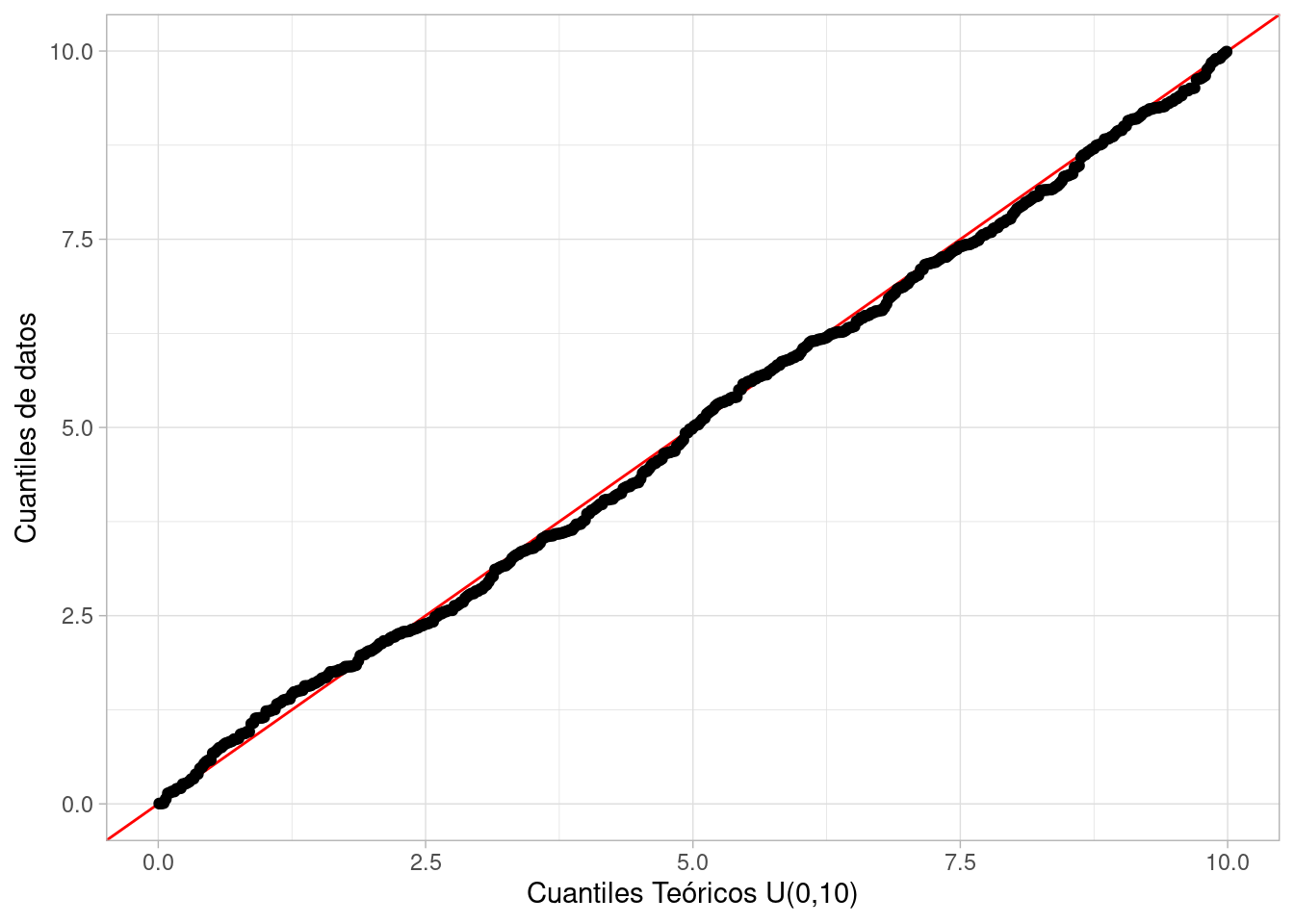 Y vemos que la forma de las dos distribuciones es muy similar: los cuantiles
empíricos son muy similares a los teóricos. Existen algunas fluctuaciones debidas
al muestreo aleatorio.
Y vemos que la forma de las dos distribuciones es muy similar: los cuantiles
empíricos son muy similares a los teóricos. Existen algunas fluctuaciones debidas
al muestreo aleatorio.7.5.2 Ejemplo: distribución triangular
Repetimos para la distribución triangular. Los cuantiles que calculamos arriba son:
qtri(c(0.25, 0.75), a = 0, b = 4)
#> [1] 1.414214 2.585786
x_sim_tri <- rtri(500, 0, 4)
ggplot(tibble(x = x_sim_tri), aes(sample = x)) +
geom_abline(colour = "red") +
geom_qq(distribution = qtri, dparams = list(a = 0, b = 4)) +
xlab("Cuantiles Teóricos triangular(0,4)") + ylab("Cuantiles de datos")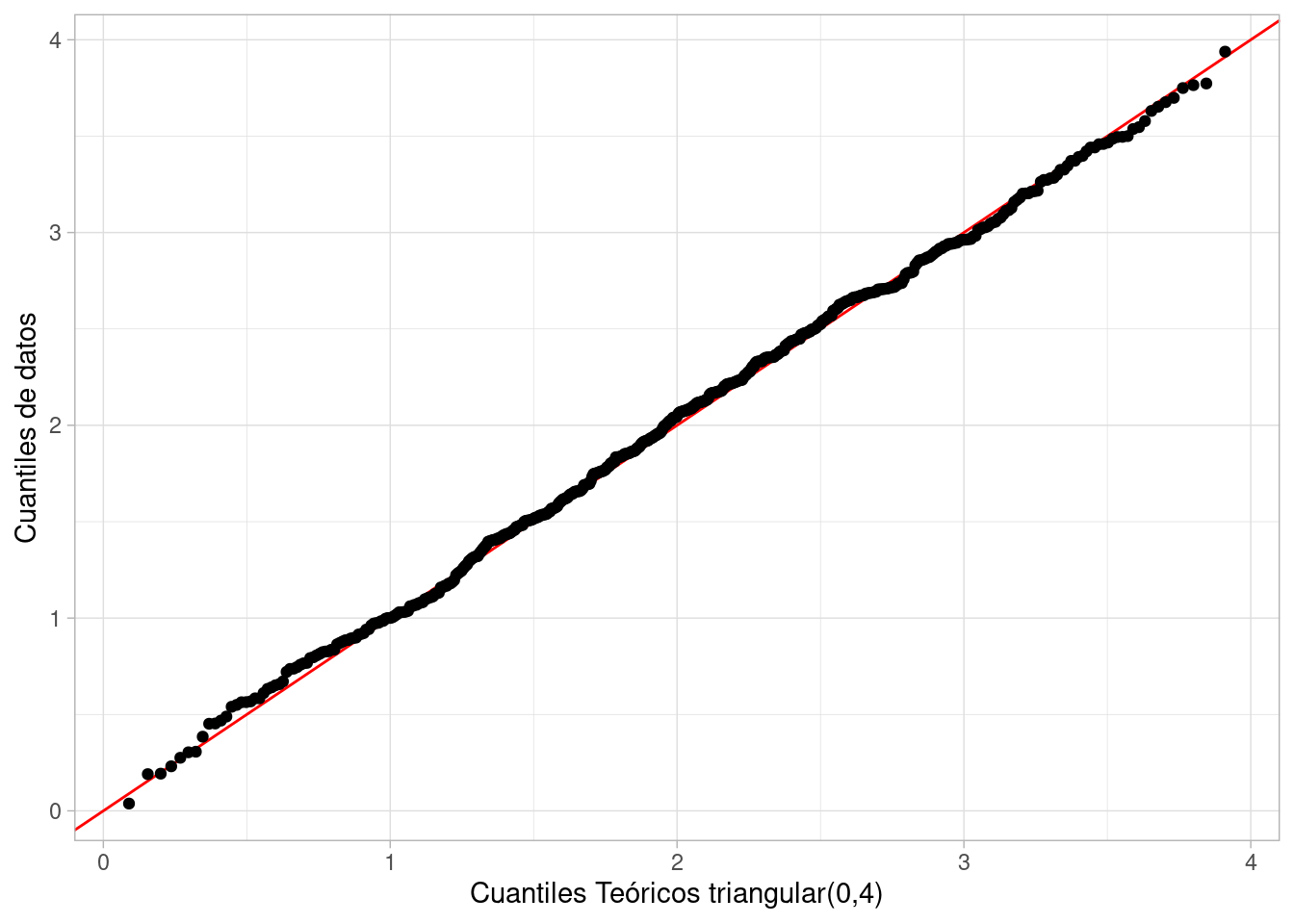 Nótese que otra vez, los cuantiles teóricos se alinean bien con los teóricos.
Nótese que otra vez, los cuantiles teóricos se alinean bien con los teóricos.7.6 Histogramas y densidades
Para el análisis de datos usual, las gráficas cuantil-cuantil tienden a ser útiles para entender si unos datos se comportan según alguna densidad teórica. Sin embargo, muchas veces se usan histogramas, como en las siguientes gráficas:
hist_1 <- ggplot(tibble(x = x_sim_u),
aes(x = x)) +
geom_histogram(aes(y = ..density..), binwidth = 1, boundary = 0) +
geom_line(data = tibble(x = seq(0, 10, 0.01)) %>%
mutate(f = dunif(x, 0, 10)),
aes(x = x, y = f), colour = "red")
hist_2 <- ggplot(tibble(x = x_sim_tri),
aes(x = x)) +
geom_histogram(aes(y = ..density..), binwidth = 0.25, boundary = 0) +
geom_line(data = tibble(x = seq(0, 4, 0.01)) %>%
mutate(f = dtri(x, 0, 4)),
aes(x = x, y = f), colour = "red")
hist_1 + hist_2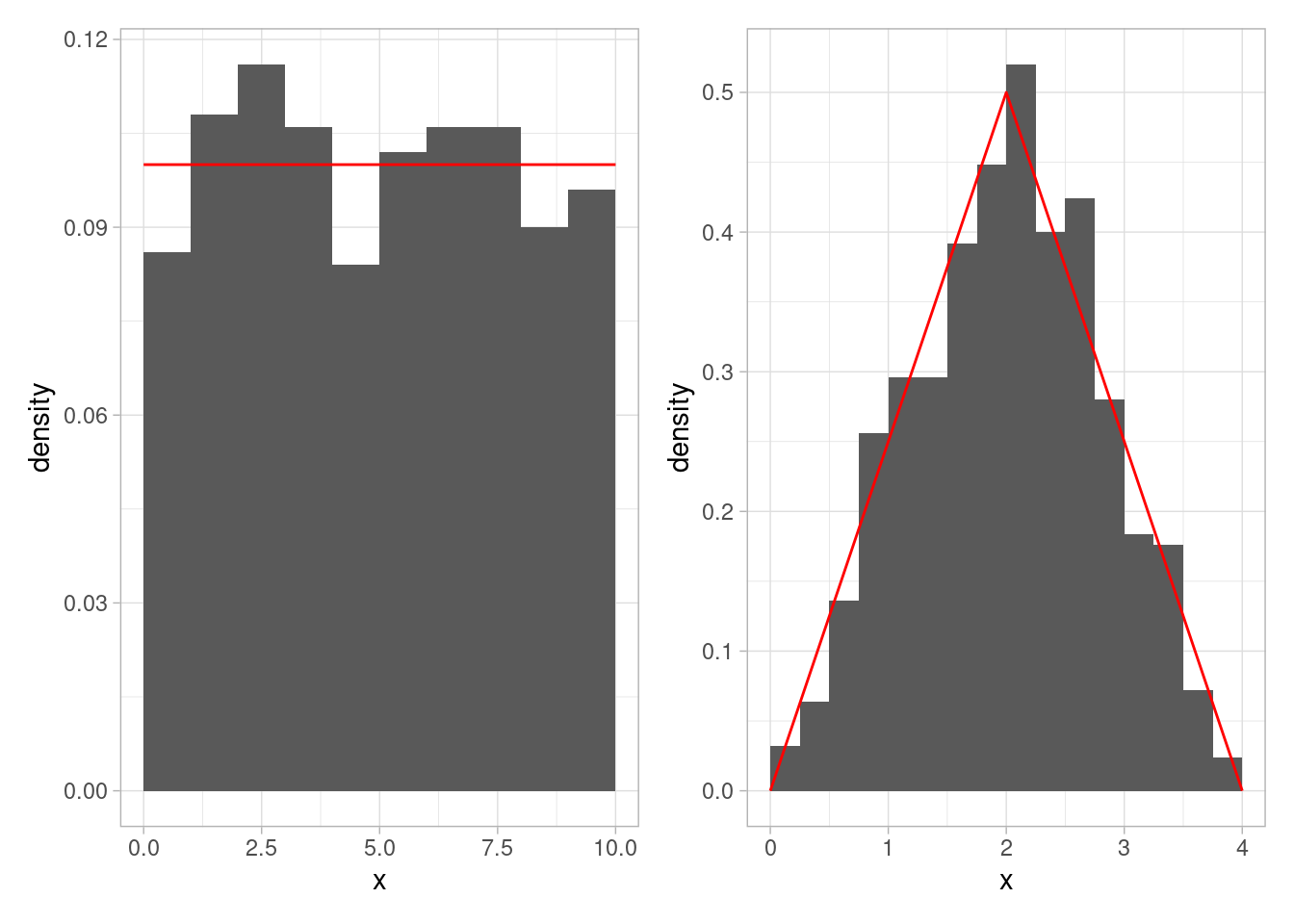
Nótese la escala vertical de estos histogramas, que no es simplemente el conteo de casos que caen en cada intervalo del histograma. Para poder comparar los conteos con las densidades correspondientes, es necesario observar lo siguiente:
Si \(I = [a,b]\) es un intervalo del histograma, según la densidad (teórica), la probabilidad de que un dato \(x\) caiga en \(I\) es \[P(x\in I) = \int_{a}^b f(x)\,dx \approx f(a) (b-a)\] La última aproximación se debe a que en un intervalo chico \([a,b]\), el área bajo la curva de \(f(x)\) es aproximadamente igual a la base (el ancho del intervalo) por la altura en un punto de la curva (\(f(a)\), aunque también podríamos usar \(f(\frac{a+b}{2})\) por ejemplo).
Si tenemos \(n\) observaciones, esperamos entonces que caigan \(nP(X\in I)\) en el intervalo \(I\), de forma que si \(n([a,b])\) es el número de observaciones que caen en \(I = [a,b]\), esperamos \[\frac{n([a,b])}{n} \approx f(a)(b-a),\] y despejando obtenemos \[f(a)\approx \frac{n([a, b])}{n(b-a)}.\] Esto implica que para aproximar la densidad, es necesario dividir las frecuencias relativas entre el ancho de los intervalos correspondientes, y de ahí la escala vertical de las gráficas de arriba.
Observación: las gráficas de cuantiles son generalmente más prácticas para evaluar el ajuste a un modelo teórico, aunque son menos comunes.
7.7 Más descriptivos: media y desviación estándar
Podemos utilizar cuantiles para describir modelos teóricos y también conjuntos de datos (por ejemplo, mediana para centralidad y diferencia entre cuantiles 0.9 y 0.10 para dispersión), y funcionan bien en general. Sin embargo, para modelos teóricos y conjuntos de datos particulares muchas veces es más conveniente usar medidas como la media y desviación estándar.
7.7.1 Media teórica y empírica
Sabemos que la media de un conjunto de datos \(x_1,x_2,\ldots,x_n\) está dada por
\[\bar{x} = \frac{x_1 + x_2 + \cdots x_n}{n}.\] Ahora consideremos qué pasa con esta cantidad cuando las \(x_i's\) son observaciones independientes de una distribución con densidad teórica \(f(x)\). Utilizaremos simulaciones de la distribución triangular que vimos arriba
datos <- tibble(x = rtri(5000, 0, 4))
ggplot(datos, aes(x = x)) + stat_bin(breaks = seq(0, 4, 0.25))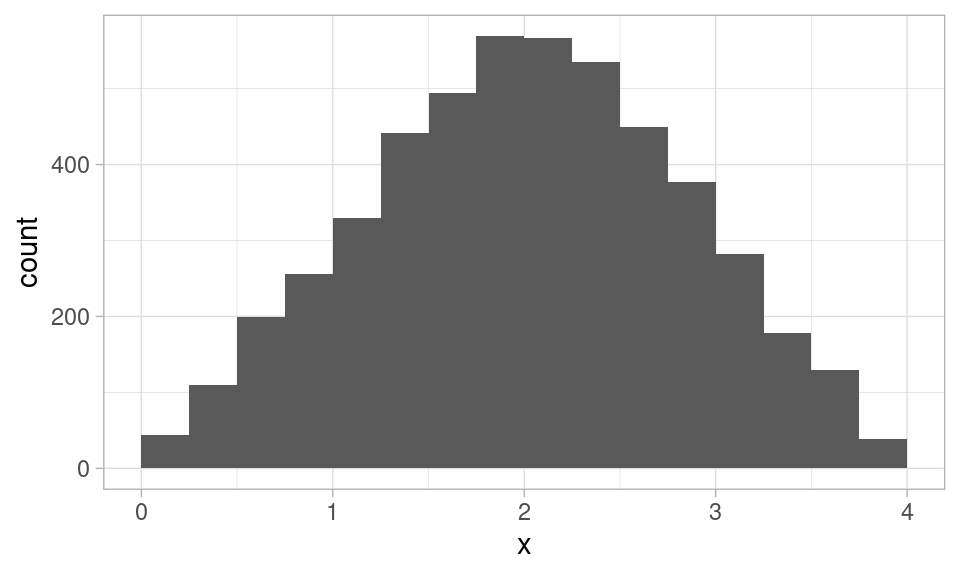
Podemos aproximar la media de estos datos promediando los valores iniciales de los intervalos de corte ponderado por el número de casos. Lo hacemos así:
particion <- seq(0, 4, 0.25)
iniciales <- head(particion, -1) # quitar último
agrupados_cubeta <- datos %>%
mutate(inicial = cut(x, breaks = particion, labels = iniciales)) %>%
mutate(inicial = as.numeric(as.character(inicial))) %>%
group_by(inicial) %>%
count() %>%
ungroup()
agrupados_cubeta
#> # A tibble: 16 x 2
#> inicial n
#> <dbl> <int>
#> 1 0 44
#> 2 0.25 110
#> 3 0.5 199
#> 4 0.75 256
#> 5 1 330
#> 6 1.25 441
#> 7 1.5 494
#> 8 1.75 569
#> 9 2 567
#> 10 2.25 535
#> 11 2.5 450
#> 12 2.75 377
#> 13 3 282
#> 14 3.25 178
#> 15 3.5 130
#> 16 3.75 38Y calculamos la aproximación a la media como sigue:
agrupados_cubeta %>%
summarise(media_aprox = sum(inicial * n) / sum(n))
#> # A tibble: 1 x 1
#> media_aprox
#> <dbl>
#> 1 1.89Apliquemos esta idea cuando tenemos una densidad \(f(x)\). Dividimos el rango de la densidad en cubetas, y aproximamos la densidad por rangos, por ejemplo:
particion <- seq(0, 4, 0.25)
valor <- dtri(particion, 0, 4)
approx_tbl <- tibble(x = particion, densidad = valor)
densidad_tri <- tibble(x = seq(0, 4, 0.01)) %>%
mutate(densidad = dtri(x, 0, 4))
ggplot(densidad_tri) +
ylab('f(x)') +
geom_line(aes(x = x, y= densidad), alpha = 0.8) +
geom_step(data = approx_tbl, aes(x = x, y = densidad), colour = "red") +
theme_minimal() 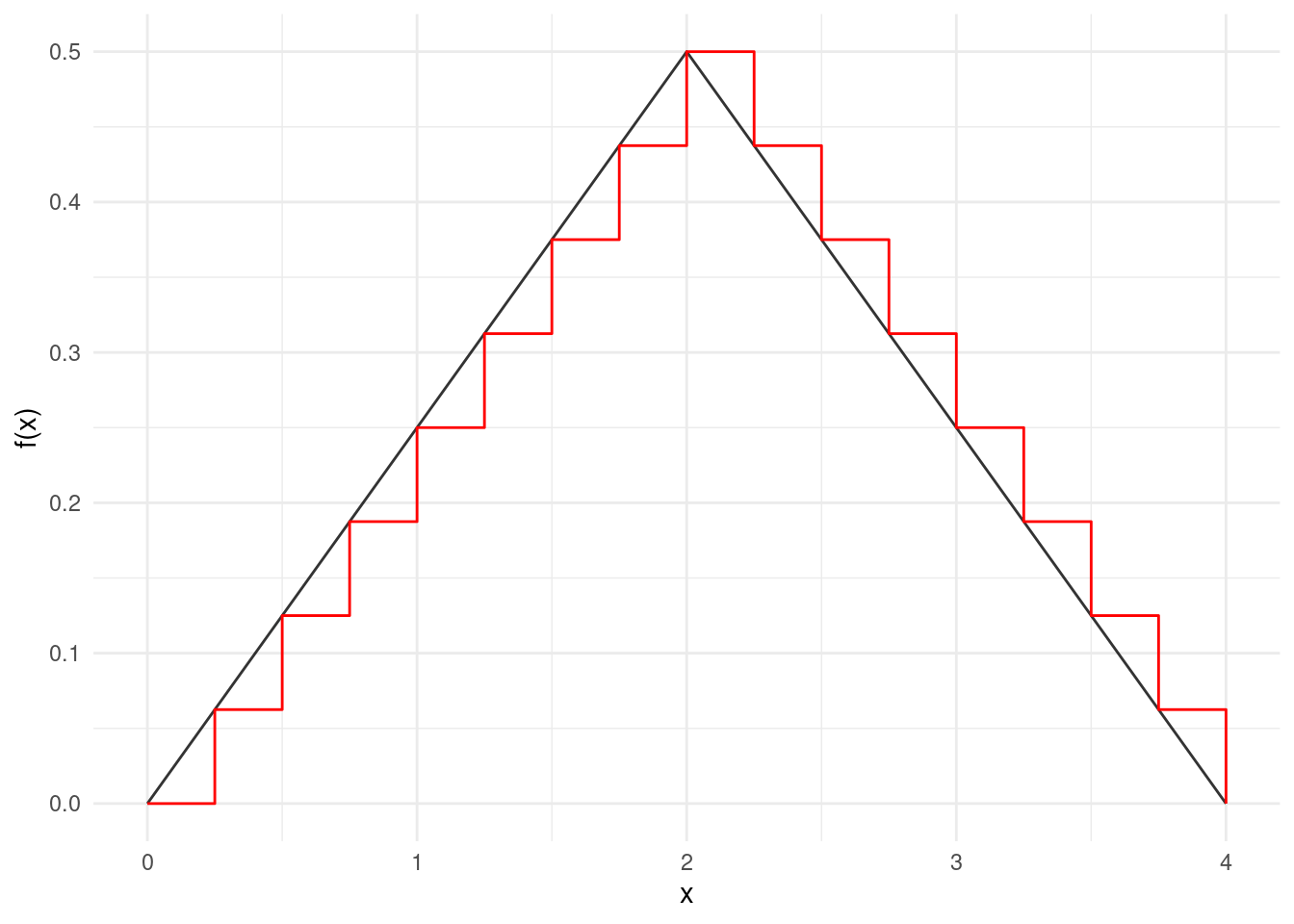
Y repetimos el mismo proceso: ponderamos los valores iniciales por la altura de la densidad:
approx_tbl %>%
summarise(media_approx = sum(x * densidad) / sum(densidad))
#> # A tibble: 1 x 1
#> media_approx
#> <dbl>
#> 1 2Y esta es una aproximación a la media de esta distribución.
Nótese que la cantidad que estamos calculando es
\[\sum_i x_i f(x_i) \Delta\]
donde \(\Delta\) es igual a
approx_tbl %>% summarise(suma_densidad = 1 / sum(densidad))
#> # A tibble: 1 x 1
#> suma_densidad
#> <dbl>
#> 1 0.25que es el ancho del intervalo de las particiones. Recordamos por cálculo que esta es una la aproximación a la siguiente integral:
\[\sum_i x_i f(x_i) \Delta \approx \int xf(x)\,dx\]
De modo que para pasar de media de los datos \(\bar{x}\) a la media de \(\mu_f\) de una distribución la equivalencia es:
\[ \bar{x} = \frac{1}{n}\sum x_i \longleftrightarrow \int xf(x) = \mu \] donde
- Usamos la densidad en lugar de frecuencias relativas para ponderar
- Usamos integral en lugar de suma
Es decir, cuando tenemos una densidad teórica continua, es necesario integrar en lugar de sumar para calcular su media.
7.7.2 Varianza y desviación estándar
Otra cantidad importante es la varianza de una muestra. Es una medida de dispersión, y se calcula como
\[ \hat{\sigma}^2 = \frac{1}{n}\sum_{i=1}^n (x_i - \bar{x})^2 \]
Nótese que cuando los datos están altamente concentrados alrededor del valor de la media, la varianza es chica, y cuando hay más dispersión alrededor de la media, la varianza es grande.
La desviación estándar es la raíz cuadrada de esta cantidad:
\[ \hat{\sigma} = \sqrt{\frac{1}{n}\sum_{i=1}^n (x_i - \bar{x})^2} \] que tiene la ventaja de que está en las mismas unidades que la variable original.
Siguiendo el mismo patrón que arriba, tenemos que integrar en lugar de sumar, y ponderar por la densidad en lugar de la frecuencia: El equivalente en una distribución teórica es también una integral, y la varianza está definida por
\[\sigma^2 = \int (x - \mu)^2 f(x) \,dx\]
La desviación estándar \(\sigma\) es la raíz cuadrada de esta cantidad.
\[\sigma = \sqrt{\int (x - \mu)^2 f(x)\,dx}\]
En resumen la densidad indica la frecuencia relativa de datos que esperamos observar alrededor de cada punto, y
- Resúmenes de una distribución teórica (como cuantiles, media, varianza, etc.) se calculan integrando ponderado por la densidad.
- Resúmenes de una distribución empírica se calculan sumando ponderando por la frecuencia relativa.
Notación
Para la media de una variable aleatoria \(X\) con densidad \(f\), utilizamos la notación siguiente:
\[\mu = \int x f(x)\,dx = E(X)\]
y decimos también que \(E(X)\) es el valor esperado de \(X\). Igualmente, la varianza podemos escribirla como el valor esperado de la variable \((X-\mu)^2\):
\[\sigma^2 = \int (x - \mu)^2 f(x) = E\left ( (X-\mu)^2 \right)\] Aunque esto requiere de un teorema simple (el teorema del estadístico inconsciente) que establece que para cualquier función \(h\), si \(Y=h(X)\) y \(f\) es la función de densidad de \(X\), entonces \[E(Y) = E(h(X)) = \int h(x) f(x) \,dx\]
7.7.3 ¿Cuándo usar media y desviación estándar?
Algunos modelos probabilísticos son más fáciles de tratar analíticamente usando media y varianza. En esos casos, conviene usar estas medidas. Esto es especialmente cierto cuando las distribuciones son simétricas y no tienen colas muy largas.
En cuanto a datos observados, conviene usar media y varianza cuando pretendemos modelarlos con densidades como las del párrafo anterior. En este caso, la interpretación de estos valores se hace a través de la forma de la densidad. Es importante checar (por ejemplo usando gráficas de cuantiles) que esas densidades describen apropiadamente a los datos.
Ejercicio
- Calcula media y desviación estándar para una densidad triangular (0,4) y otra (0,10)
- Calcula media y desviación estándar para una densidad uniforme en (0,4) y otra uniforme en (0, 10)
- Contrasta tus resultados. ¿Las medias ocurren en el lugar que esperabas? ¿Qué distribuciones presentan más dispersión de acuerdo a la desviacion estándar?
7.8 La distribución normal
La distribución normal es una que aparece naturalmente en al teoría de probabilidad.
7.8.1 Promedio de variables
Consideremos que tiramos 40 dados justos de 6 lados, y consideramos su promedio \(\bar{X}\) como resultado de nuestro experimento aleatorio. ¿Cómo se ve la distribución de probabilidades de esta variable \(\bar{X}\)?
Comenzamos haciendo simulacion:
simular_bolsa <- function(num_dados = 40){
dados <- sample(1:6, num_dados, replace = TRUE)
media <- mean(dados)
media
}
simular_bolsa()
#> [1] 3.85Veamos cómo se ven los resultados si hacemos este experimento un número grande de veces:
set.seed(23)
sims_dados <- map_dbl(1:10000, ~ simular_bolsa())
ggplot(tibble(resultado = sims_dados),
aes(x = resultado)) +
geom_histogram(binwidth = 0.1)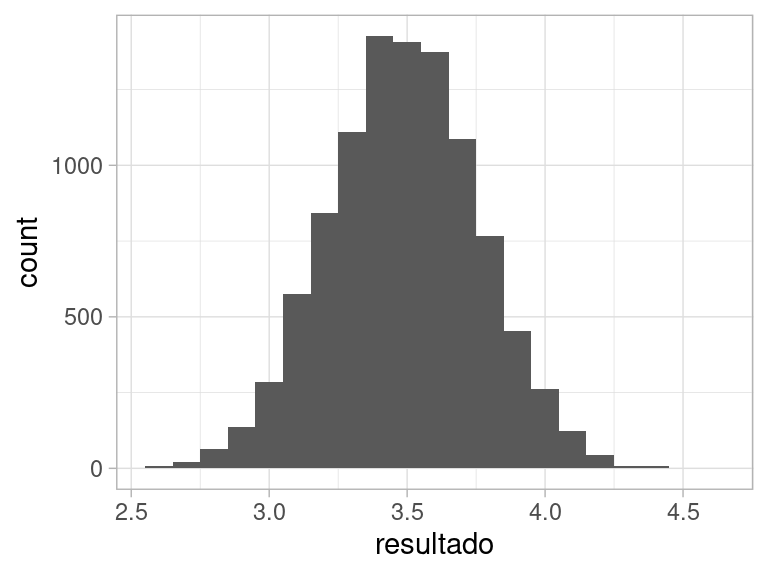
Y notamos una forma de “campana” interesante. Esto se explica porque típicamente tendremos tiros bajos y altos, de modo que muchos resultados de este experimento se concentran alrededor de la media de un dado (3.5). Además, existen fluctuaciones aleatorios, y a veces tenemos un poco más de tiros altos o de tiros bajos, de forma que existe dispersión alrededor de 3.5.
Sin embargo, estas desviaciones de 3.5 no pueden ser muy grandes: por ejemplo, para tener un promedio de 1, todas las tiradas de los 40 dados tendrían que dar 1, y eso es muy poco probable. Igualmente, para que el promedio fuera cercano a 6, la gran mayoría de los 40 dados deberían de dar 6, lo cual otra vez es muy poco probable. Esto explica al menos la forma general de la forma de las colas derecha e izquierda de esta distribución.
Los dados podrían ser diferentes (por ejemplo, un poco cargados a 1 o 6, o más cargados a valores centrales), y los argumentos de arriba también se cumplirían. Lo que es sorprendente es que, independientemente de cómo sean las particularidades de los dados, la forma analítica de esta distribución que acabamos de mostrar es la misma.
Esta forma está descrita por la densidad normal estándar:
\[f(x) = \frac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}}\]
cuya gráfica presentamos a continuación:
tibble(x = seq(-3.5, 3.5, 0.01)) %>%
mutate(f = (1/sqrt(2*pi)) * exp(-x^2 / 2)) %>%
ggplot(aes(x = x, y = f)) + geom_line()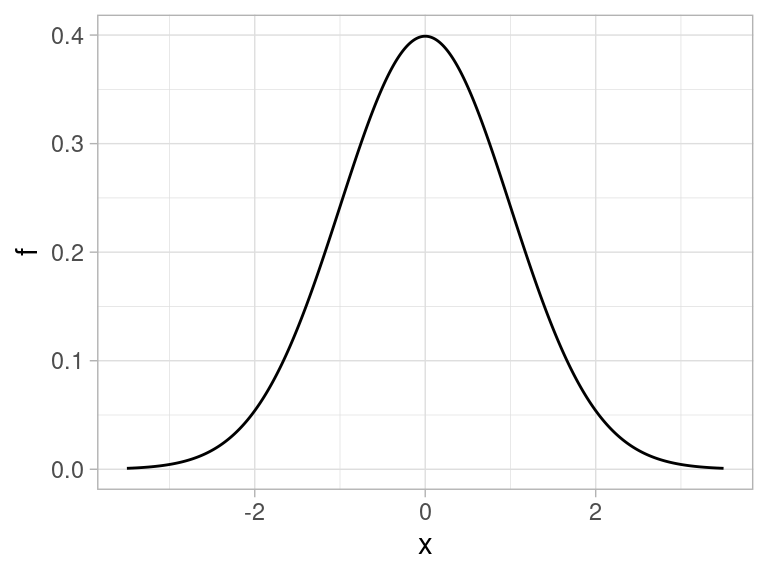
A una variable \(Z\) que tiene esta densidad le llamamos una variable con distribución normal estándar. Comparemos cuantiles en nuestro ejemplo:
ggplot(tibble(resultado = sims_dados),
aes(sample = resultado)) +
geom_qq(distribution = stats::qnorm) +
xlab("Normal estándar teórica") +
ylab("Promedio de 40 dados")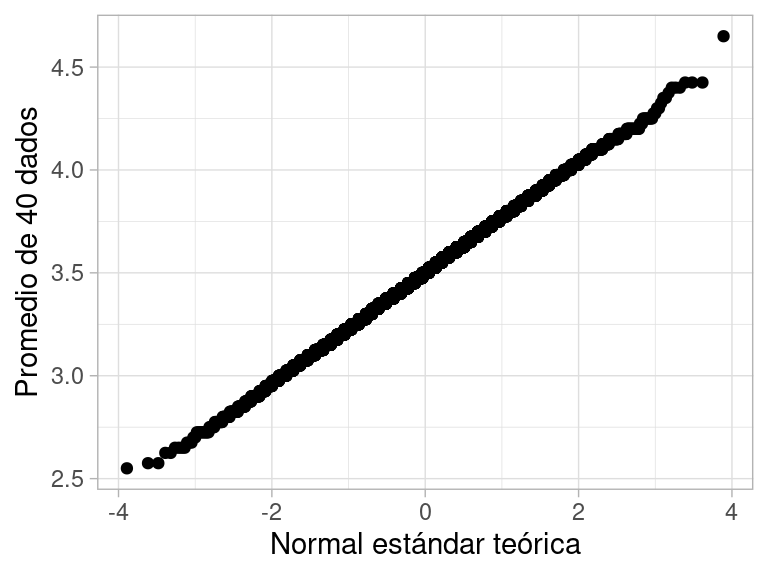 Y notamos que los cuantiles no corresponden, pero el espaciamiento entre los cuantiles
de los datos y los teóricos de la normal estándar es el mismo. Quiere decir que
estas dos distribuciones tienen la misma forma, aunque estén escaladas y centradas en distintos valores.
Y notamos que los cuantiles no corresponden, pero el espaciamiento entre los cuantiles
de los datos y los teóricos de la normal estándar es el mismo. Quiere decir que
estas dos distribuciones tienen la misma forma, aunque estén escaladas y centradas en distintos valores.
Probemos con promedios de 20 observaciones triangulares en \((0,1)\) por ejemplo. El resultado es el mismo:
set.seed(23)
sims_tri <- map_dbl(1:10000, ~ mean(rtri(20, 0 ,1)))
ggplot(tibble(resultado = sims_tri),
aes(x = resultado)) +
geom_histogram(binwidth = 0.01)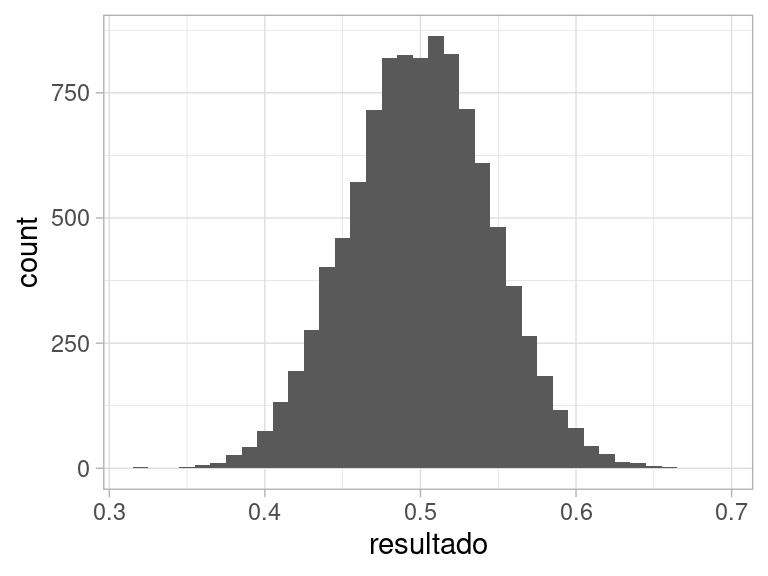
ggplot(tibble(resultado = sims_tri),
aes(sample = resultado)) +
geom_qq(distribution = stats::qnorm) +
xlab("Normal estándar teórica") +
ylab("Promedio de 20 triangulares (0,1)")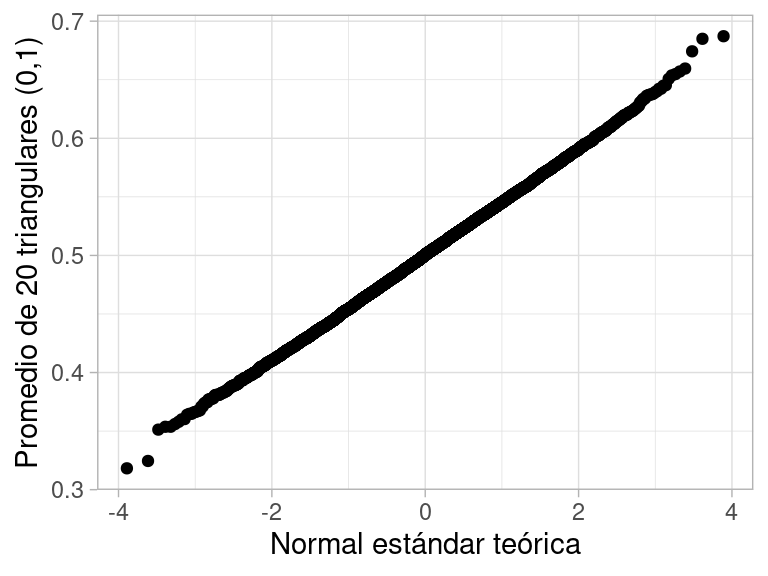 Otra vez, la forma general es la misma, aún cuando los datos están centrados
y escalados de manera distinta.
Otra vez, la forma general es la misma, aún cuando los datos están centrados
y escalados de manera distinta.7.9 La densidad normal estándar
Como expicamos, la densidad normal estándar está dada por
\[f(x) = \frac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}},\]
cuya gráfica es como sigue:
normal_std_graf <- tibble(x = seq(-3.5, 3.5, 0.01)) %>%
mutate(f = dnorm(x, 0, 1))
ggplot(normal_std_graf, aes(x = x, y = f)) +
geom_line()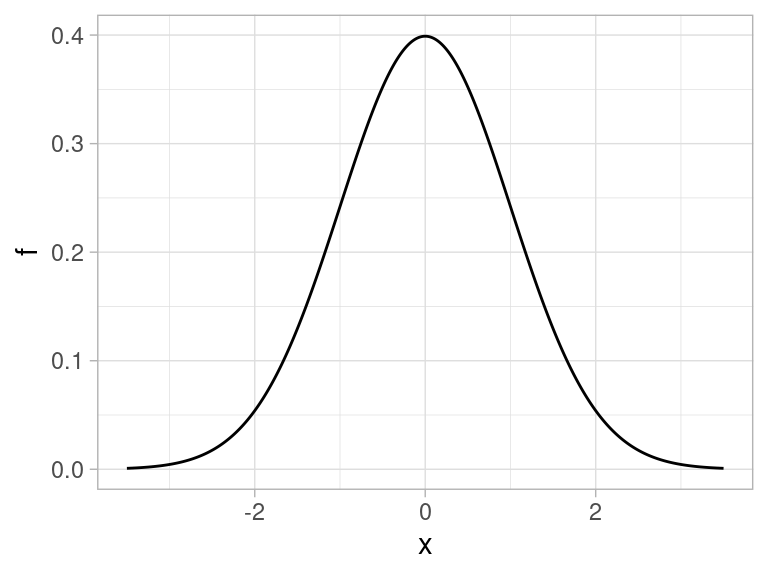 Las probabilidades asociadas a una normal estándar se calculan integrando
esta curva (que tiene que hacerse de forma numérica). Por ejemplo,
para calcular
Las probabilidades asociadas a una normal estándar se calculan integrando
esta curva (que tiene que hacerse de forma numérica). Por ejemplo,
para calcular\[P(Z < 1.5),\] podemos usar
pnorm(1.5)
#> [1] 0.9331928Que es el área bajo la curva mostrada abajo:
normal_std_graf <- tibble(x = seq(-3.5, 3.5, 0.005)) %>%
mutate(f = dnorm(x, 0, 1))
ggplot(normal_std_graf, aes(x = x, y = f)) +
geom_line() +
geom_area(aes(x = ifelse(x > -3.5 & x < 1.5, x, 0)),
fill="salmon", alpha = 0.5) +
ylim(c(0,0.4)) +
scale_x_continuous(breaks = seq(-3.5, 3.5, 0.5))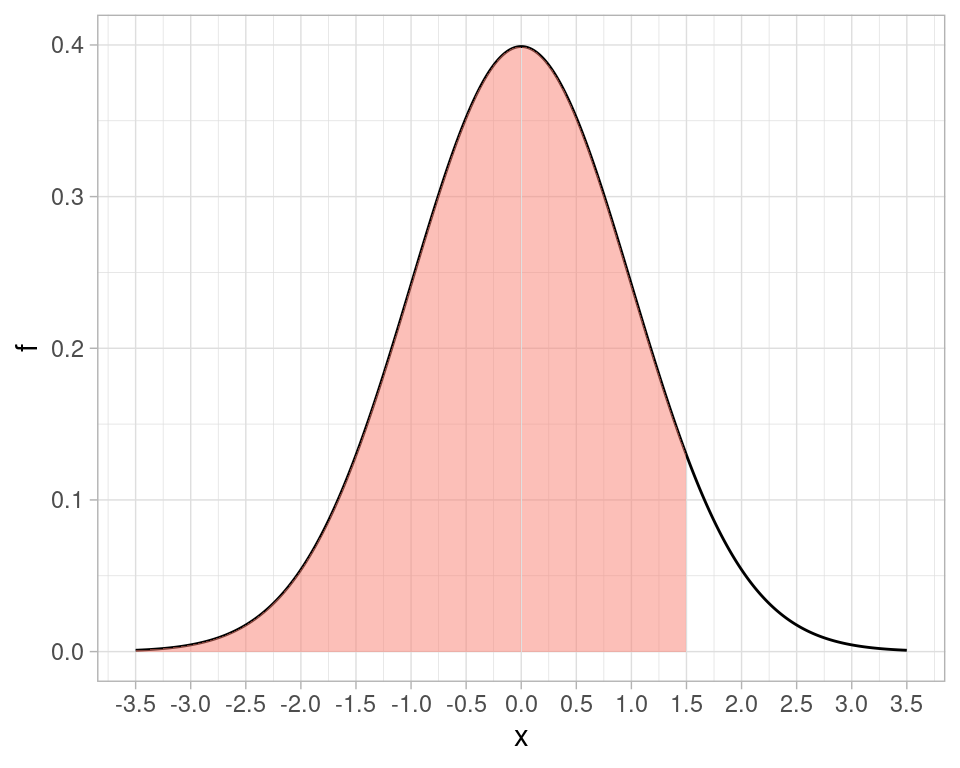
Esta es la forma de la densidad estándar. Podemos centrar esta campana en otro valor \(\mu\) y aumentar la dispersión por un factor \(\sigma\). Si \(Z\) es una variable normal estándar, la variable
\[X = \mu + \sigma Z\]
es una variable normal con parámetros \((\mu, \sigma)\), o de manera más compacta, decimos que \(X\) es \(N(\mu, \sigma)\). La distribución normal estándar es \(N(0,1)\).
Por ejemplo, si escogemos \(\mu=5\) y \(\sigma = 0.5\), obtenemos:
normal_graf <- tibble(x = seq(3, 7, 0.01)) %>%
mutate(f = dnorm(x, 5, 0.5))
ggplot(normal_graf, aes(x = x, y = f)) +
geom_line()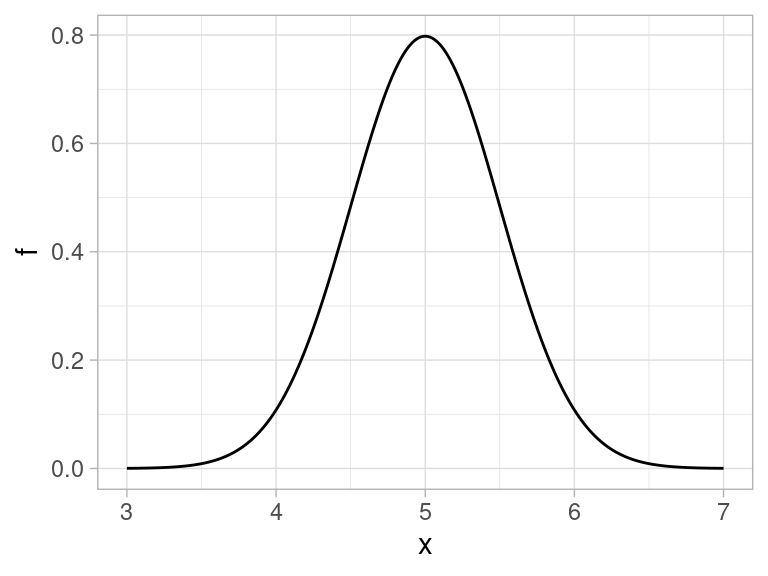
Podemos mostrar juntas estas dos distribuciones:
densidad_normal <- tibble(x = seq(3, 7, 0.1)) %>%
mutate(densidad = dnorm(x, 5, 0.5))
densidad_normal_estandar <- tibble(x = seq(-3, 3, 0.1)) %>%
mutate(densidad = dnorm(x))
g_2 <- ggplot(densidad_normal_estandar, aes(x = x, y = densidad)) + geom_line()
g_3 <- g_2 + xlim(c(-3, 7)) + ylim(c(0, 1))
g_1 <- ggplot(densidad_normal, aes(x = x, y = densidad)) + geom_line() + xlim(c(-3, 7)) + ylim(c(0, 1))
g_3 + g_1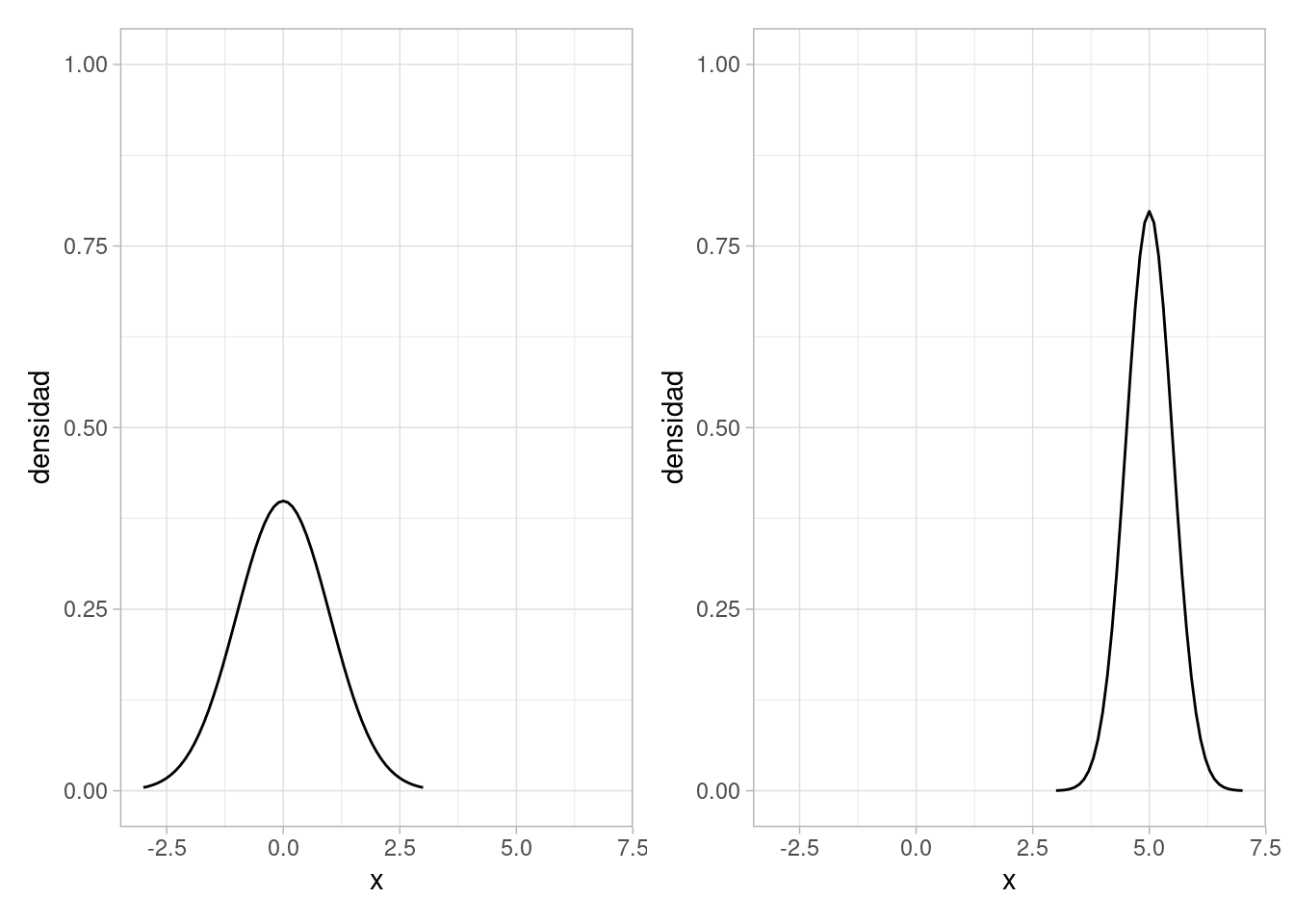
Se puede demostrar que:
Distribución normal
- La distribución normal estándar \(N(0,1)\) tiene media 0 y desviación estándar 1
- La distribución normal \(N(\mu,\sigma)\) tiene media \(\mu\) y desviación estándar \(\sigma\)
7.10 Cuantiles y concentración de la densidad normal
Con un poco de cálculo podemos ver qué tan fuertemente se concentra la densidad alrededor de la media para una distribución normal. La regla es la siguiente:
- 68% de la densidad se concentra en el intervalo \([\mu-\sigma, \mu+\sigma]\)
- 95% de la densidad se concentra en el intervalo \([\mu-2\sigma, \mu+2\sigma]\)
- 99.7% de la densidad se concentra en el intervalo \([\mu-3\sigma, \mu+3\sigma]\)
grafica_concentracion <- function(mu, sigma, z){
x <- seq(mu - 3.1 * sigma, mu + 3.1 * sigma, 0.01)
valor <- dnorm(x, mu, sigma)
datos <- tibble(x = x, `f(x)`=valor)
texto <- round(100*(pnorm(z) - pnorm(-z)), 1)
texto <- paste0(texto, "%")
ggplot(datos, aes(x = x, y = `f(x)`)) +
geom_area(data = filter(datos, x < mu + z*sigma, x > mu - z*sigma),
fill = "salmon") +
geom_line() +
annotate("text", x = mu, y = 0.1, label = texto) +
scale_x_continuous(breaks = mu + sigma*seq(-3, 3, 1)) +
theme_minimal() + ylab("")
}
g_68 <- grafica_concentracion(10, 2, 1)
g_95 <- grafica_concentracion(10, 2, 2)
g_997 <- grafica_concentracion(10, 2, 3)
paneles <- g_68 + g_95 + g_997
paneles + plot_annotation(title = "Concentración alrededor de la media (normal)")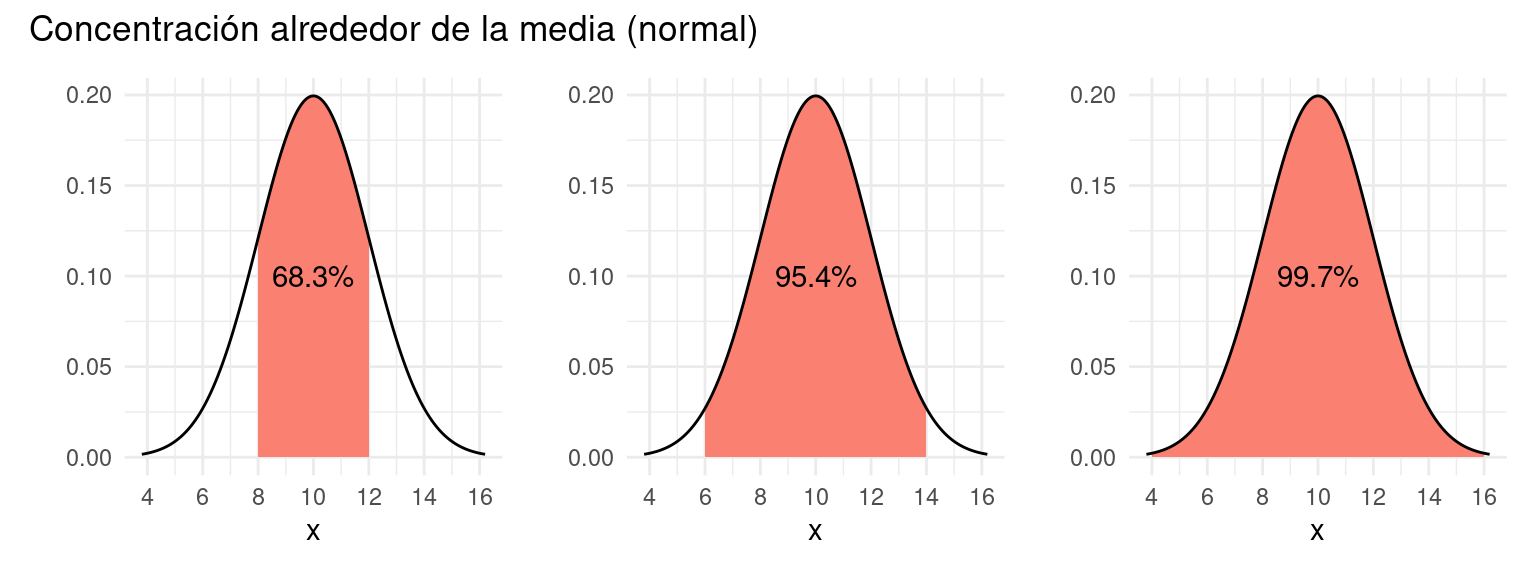
Nota: esto aplica para cualquier densidad normal, independientemente de los parámetros.
Obsérvese que esto nos da una interpretación natural de la desviación estándar de una distribución normal en términos de percentiles de los datos, y la manera usual con la que entendemos la desviación estándar de la distribución normal.
7.11 El teorema central del límite
Una de las razones por las que el modelo normal es tan importante es el siguiente resultado:
Teorema central del límite
Si \(X_1,X_2,\ldots, X_n\) son variables aleatorias independientes con media \(\mu\) y desviación estándar \(\sigma\) con una densidad \(f(x)\):
- \(S_n = X_1 + X_2 + \cdots X_n\) es aproximadamente normal cuando \(n\) es suficientemente grande
Esto nos permite, por ejemplo, considerar nuestro primera técnica de estimación por intervalos:
Observamos una muestra grande \(x_1,\ldots, x_n\) de datos de una población (no necesariamente con distribución normal). Supongamos que buscamos estimar la media \(\mu\) de la población con un intervalo.
Estimamos la media con \[\bar{x} = \frac{1}{n}(x_1+\cdots + x_n) = \frac{1}{n}\sum_i x_i,\]
Por el teorema del límite central, {x} es aproximadamente normal, y su media es \(\mu\). Esto implica que
\[P(\mu - 2\sigma \leq \bar{x} \leq\mu + 2\sigma)\approx 0.95\] Despejando \(\mu\) obtenemos \[P(\bar{x} - 2\sigma \leq \mu \leq\bar{x} + 2\sigma)\approx 0.95\] Finalmente, no conocemos \(\sigma\), pero la estimamos con
\[\hat{\sigma}^2 = \frac{1}{n}((x_1 - \bar{x})^2 + \dots + (x_n - \bar{x})^2) = \frac{1}{n}\sum_i(x_i - \bar{x})^2\]
Y aproximamos sustituyendo nuestra estimación:
\[P(\bar{x} - 2\hat{\sigma } \leq \mu \leq\bar{x} + 2\hat{\sigma})\approx 0.95\] Esto nos da un intervalo (llamado el intervalo de Wald) con 95% de confianza para la media poblacional:
\[[\bar{x} - 2\hat{\sigma } , \bar{x} + 2\hat{\sigma}]\] Notas:
- Por otras razones técnicas, a veces se usa \(s^2 = \frac{1}{n-1}\sum_i (x_i-\bar{x})^2\) en lugar de \(\hat{\sigma}^2\). Si la muestra es grande esto no es importante.
- Estos intervalos tienen cobertura nominal de 95%, sin embargo, puede variar dependiendo del tamaño de muestra y la forma de la distribución teórica (poblacional). Existen métodos como el bootstrap donde podemos checar qué tan razonable es hacer esta aproximación. También se puede hacer simulación modelando la distribución \(f(x)\).
7.12 Otras densidades comunes
Como vimos arriba, consideraciones teóricas hacen razonable suponer que una variable aleatoria tiene cierta distribución: por ejemplo, si una variable aleatoria es suma de muchas perturbaciones independientes, la suma o promedio resultante puede modelarse como una distribución normal.
Otras consideraciones teóricas sugieren otro tipo formas útiles de densidades. Un primer ejemplo es la distribución exponencial.
7.12.1 Variables aleatorias exponenciales
Supongamos que estamos modelando tiempos a la ocurrencia \(X\) de un evento (por ejemplo en análisis de supervivencia en estudios clínicos). Esta es una variable que toma valores en los números positivos. ¿Cómo podría ser su forma?
Consideremos por ejemplo que el tiempo de espera no tienen memoria. Es decir: si hay esperamos un periodo de \(t\) días por ejemplo, la distribución del tiempo restante que tenemos que esperar no depende de \(s\). En términos de probabilidad, podríamos escribir: \[P(X > s + t | X > t) = P(X > s)\] Esto se lee: dado que el evento ocurre en más de \(t\) días, la probabilidad de que tarde al menos otros \(s\) días no dependen de \(t\). A la función \(S(t) = P(X>t)\) muchas veces se le llama la función de supervivencia.
Este es un modelo base útil, que después puede extenderse a procesos donde los eventos ocurren aceleradamente (envejecen), o donde los eventos dan evidencia de robustez (los que han sobrevivido hasta cierto tiempo se espera que duren más que lo que inicialmente), o quizá una combinación de los dos dependiendo de el valor de \(t\).
Con el supuesto de falta de memoria, la ecuación de arriba se cumple, y entonces (¿por qué?): \[P(X > s + t) = P(X > s) P(X > t),\] así que \[\frac{1}{s}(P(X > s+ t) - P(X>t)) = \frac{1}{s}(P(X>s) - 1)P(X>t).\] Que podemos reescribir usando la densidad \(f(x)\) como \[\frac{1}{s}\int_t^{t+s} f(x)\,dx = P(X>t)\frac{1}{s}\int_0^s f(x)\,dx\] Conforme \(s\) se hace más chica, el lado izquierdo converge a \(f(t)\). El lado derecho, por otra parte, converge a \(f(0)\), y obtenemos \[f(t) = f(0)\int_t^\infty f(x)\,dx,\] y ahora derivamos de ambos lados para obtener \[f'(t) = -f(0)f(t)\] La única función que satisface esta propiedad (su derivada es proporcional a ella misma) es \[f(t) = \lambda e^{-\lambda t}\] Puedes checar que efectivamente esta densidad cumple que la ecuación anterior. A esta densidad le llamamos la densidad exponencial con tasa \(\lambda\).
lambda <- 1
sim_exp <- rexp(1000, rate = lambda)
ggplot(tibble(x = sim_exp), aes(x = x)) +
geom_histogram(boundary = 0)
#> `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.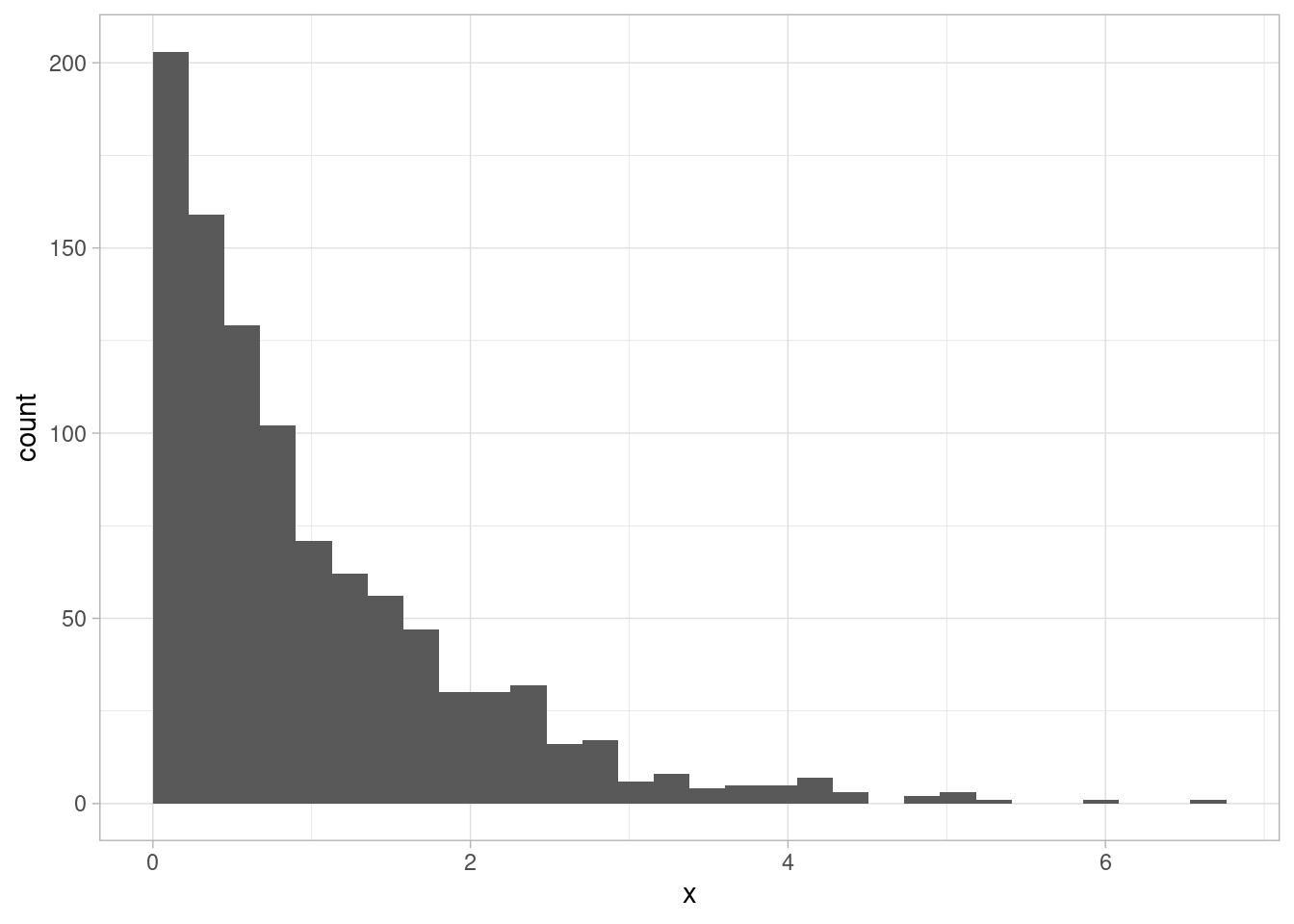
Ejercicio: demuestra que una variable aleatoria exponencial con tasa \(\lambda\) tiene media \(E(X) = 1/\lambda\) y $Var(X) = 1 / ^2
El parámetro \(\lambda\) se llama tasa por la interpretación de tiempo de espera que mostramos arriba. Supongamos que \(\lambda = 10\). Eso quiere decir que esperamos observar el evento en \(1/\lambda = 1/10\) minutos, por ejemplo, o lo que es lo mismo, a una tasa de \(\lambda = 10\) eventos por minuto.
Nótese finalmente que todas las variables exponenciales son escalamientos de una variable exponencial con \(\lambda = 1\). Esto es porque si \(Y=kX\), y \(X\) es exponencial con \(\lambda= 1\) entonces:
\[P(Y>t)=P(kX > t) = P(X > t/k) = \int_{t/k}^\infty e^{-x}\,dx = e^{-t/k}\] De modo que derivando, encontramos que la densidad de \(Y\) es \(\frac{1}{k} e^{-t/k}\), que es una exponencial con tasa \(\lambda = 1/k\).
7.12.2 Ejemplo: exponencial
Supongamos que un tipo de focos tienen tiempos de vida exponencial con una vida media de 10 años. ¿Cuál es la probabilidad de que un foco dure más de 15 años? Si tenemos un foco que ya vivió 10 años, cuál es la probabilidad de que dure otros 15 años.
Tenemos que la vida de un foco es una variable \(X\) exponencial con parámetro \(\lambda = 1/10\). La probabilidad de que dure más de 15 años es entonces \[P(X>15) = \int_{15}^\infty \frac{1}{10} e^{x/10}\,dx\]
Podemos calcular a mano, o usar rutinas usuales de R:
pexp(15, rate = 1/10, lower.tail = FALSE)
#> [1] 0.22313027.12.3 Variables aleatorias gamma
Esta es otra familia que extiende la familia de distribuciones exponenciales. La forma analítica de una densidad gamma con parámetro de forma \(k>0\) y tasa \(\lambda\)
\[f(x) = C x^{k-1} e^{-\lambda x}\] donde la constante \(C\) de normalización depende de \(k\) y \(\lambda\).
Abajo vemos datos simulados de densidades Gamma con distintas combinaciones de parámetros:
params_tbl <- crossing(k = c(1, 2, 5, 10), lambda = c(1/4, 1/2))
sims_tbl <- params_tbl %>%
mutate(sims = map2(k, lambda,
~ rgamma(10000, shape = .x, rate = .y))) %>%
unnest(cols = sims)
ggplot(sims_tbl, aes(x = sims)) +
geom_histogram(boundary = 0, bins = 50) +
facet_grid(k~lambda)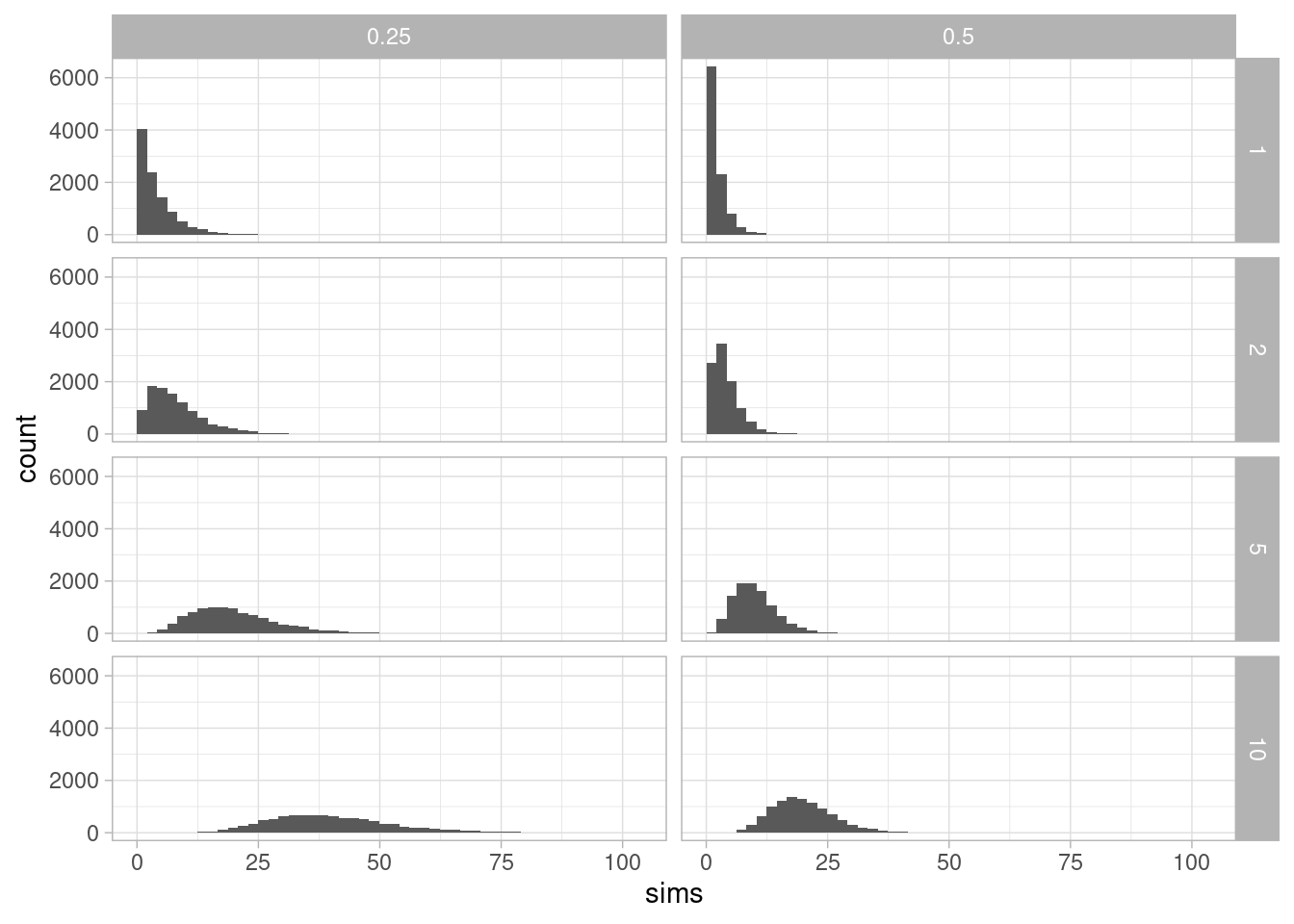
Nótese que cada columna es un rescalamiento de la otra, pero las densidades de los renglones tienen distinta forma. Puedes ver aquí parámetros como esperanza, varianza de esta estas distribuciones, junto con otras propiedades y aplicaciones.