8 Modelos conjuntos de probabilidad
Usualmente no nos interesa una sola variable aleatoria, sino varias. Nos interesa entender cómo están relacionadas o cómo depende una de otra.
Por ejemplo, ¿cuál es la mediana de peso para un infante de 2 meses, y qué tan diferente es de la mediana de peso para un infante de 5 meses? ¿qué relación hay entre temperatura y presión atmosférica? ¿qué relación hay entre creencias religiosas y afiliación política? En todos estos casos quisiéramos describir de distintas formas cómo ser relaciona una cantidad aleatoria con otra.
Al principio de este curso, vimos algunas técnicas descriptivas para mostrar y explorar estas relaciones en datos observados. Por ejemplo:
- ¿Cómo cambian las preferencias de forma de tomar té dependiendo del tipo de té una persona acostumbra tomar? ¿Qué tan probable es que alguien que toma té negro use azúcar vs alguien que toma té verde? (relación entre dos variables categóricas o discretas)
- ¿Cómo cambian los precios medios de las casas dependiendo del vecindario donde se ubican? (describir la dependencia de una variable numérica si sabemos el valor de una variable categórica)
- ¿Cómo cambia la mediana y los cuartiles de peso de un infante dependiendo de los meses desde que nació (describir cómo depende una variable numérica de otra variable numérica)
En esta parte veremos una introducción cómo se formalizan estos conceptos en modelos probabilísticos.
8.1 Estaturas: modelando relaciones de dependencia
Supongamos que \(X\) es la edad de una persona entre 4 y 15 años. y \(Y\) es su estatura. La relación entre \(X\) y \(Y\) no es determinística, pues existe variación en el crecimiento para las personas por distintas razones. Por esta razón, no tiene mucho sentido dar una relación como \(Y = 80 + 5.5 X\), por ejemplo, pues esta relación no se cumple para prácticamente ninguna persona.
Tiene más sentido, sin embargo, decir cómo es la distribución condicional de \(Y\) dado que conocemos \(X\). Por ejemplo, podríamos hacer la hipótesis de que la mediana de estatura para una persona de edad \(X\) está dada por \[med(Y|X) = 80 + 5.5 X\] Nótese que escribimos la mediana condicional de \(Y\) dado que conocemos el valor de \(X\). También podríamos escribir la media condicional de \(Y\) dada \(X\) como
\[E(Y|X) = 80 + 5.5 X\] Y estas dos cantidades tienen sentido.
Estas cantidades claramente no determinan la variabilidad que hay de la estatura cuando conocemos \(X\). Podríamos entonces también especificar por ejemplo la desviación estándar condicional:
\[\sigma(Y|X) = 3\sqrt{X} \] Generalmente estas relaciones se estiman empíricamente con datos observados, pero para este ejemplo utilizaremos estos modelos fijos.
Simulamos algunos datos con estas propiedades:
edades <- runif(800, 2, 15) # edad distribuida uniforme, o grupos de edad del mismo tamaño
datos_tbl <-
tibble(edad = edades) %>%
mutate(media = 80 + 5.5*edad, desv_est = 3 * sqrt(edad)) %>%
# para este ejemplo, simulamos con la distribución normal.
mutate(estatura_cm = rnorm(n(), mean = media, sd = desv_est))
ggplot(datos_tbl, aes(x = edad, y = estatura_cm)) +
geom_point()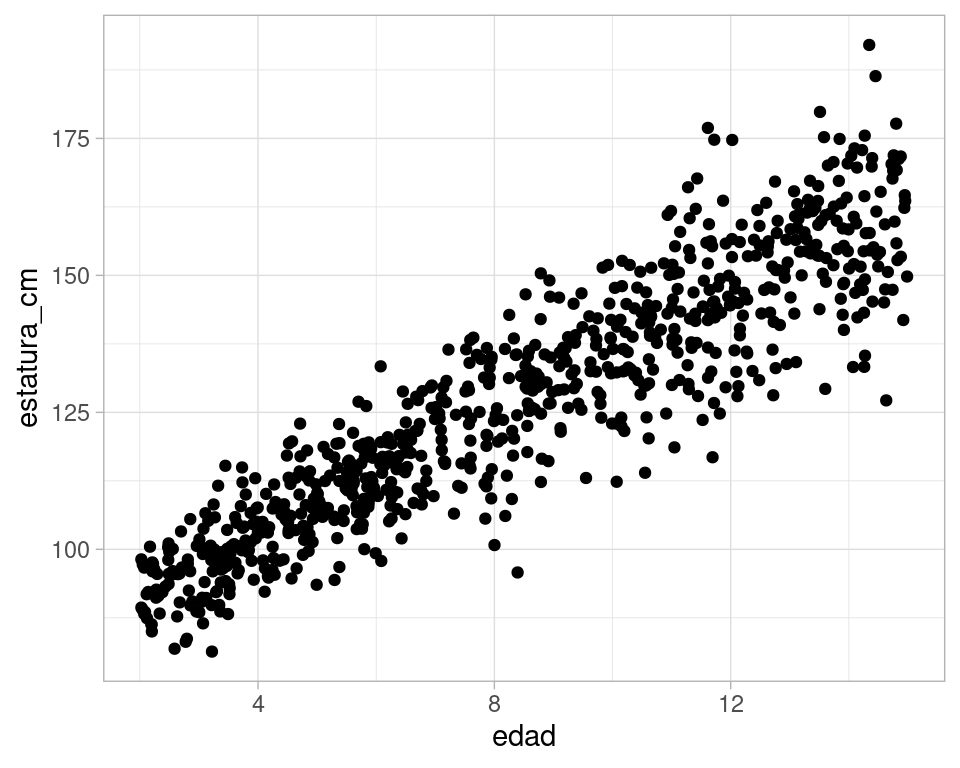
- Obsérvese cómo en efecto la estatura esperada aumenta con la edad (condicional a la edad), y que la dispersión de estatura aumenta conforme la edad aumenta.
- Nótese adicionalmente que para poder tener un modelo completo del que podemos simular, tuvimos que establecer no solamente medias y varianzas condicionales, sino también la densidad condicional especifica. En este caso utilizamos la normal con media y varianza condicionales que decidimos arriba.
Nótese que si usamos un suavizador, podemos estimar la media condicional de nuestro modelo, que en este caso está cercana a la fórmula que establecimos en nuestro modelo:
ggplot(datos_tbl, aes(x = edad, y = estatura_cm)) +
geom_point() +
geom_smooth(se = FALSE)
#> `geom_smooth()` using method = 'loess' and formula 'y ~ x'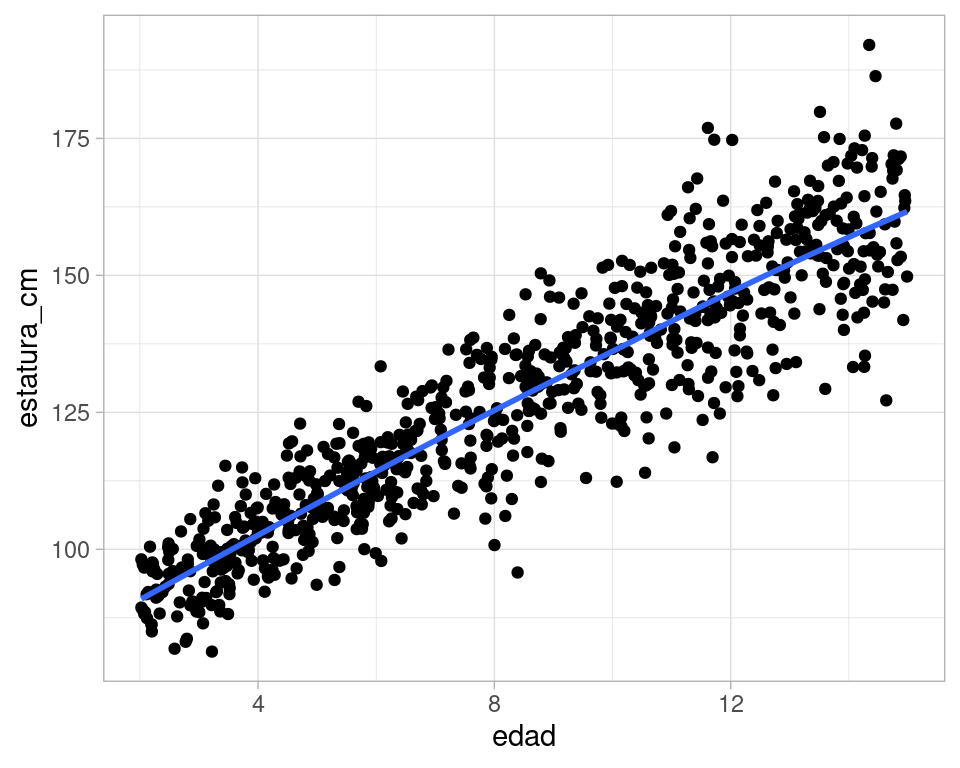
Podemos estimar cuantiles también como vimos en secciones anteriores:
ggplot(datos_tbl, aes(x = edad, y = estatura_cm)) +
geom_point() +
geom_quantile(method = "rqss", lambda = 20, quantiles = c(0.10, 0.5, 0.90))
#> Smoothing formula not specified. Using: y ~ qss(x, lambda = 20)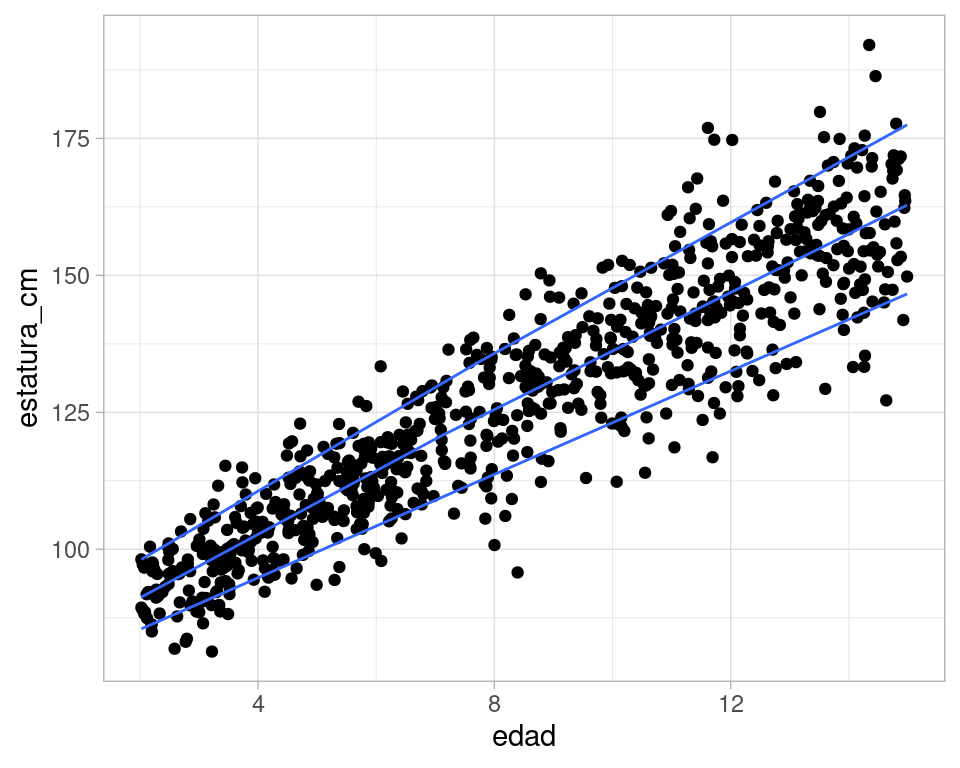
Y observamos igualmente que la dispersión para el grupo de 15 años es cercana al doble que la dispersión para el grupo de 4 años.
8.2 Distribuciones condicionales
Todo el trabajo de arriba de modelación teórica consiste entonces en definir distribuciones condicionales. En el ejemplo anterior,
- Dimos una distribución para \(X\), que en este caso la tomamos uniforme en [4, 15], pues suponemos que esta es la estructura de nuestra población (hay el aproximadamente el mismo número de personas de cada edad)
- Dimos una distribución para \(Y\) condicionada a \(X\). En este caso, establecimos que \(Y|X\) es normal con media \(80 + 5.5X\) y desviación estándar \(3 * sqrt(X)\).
Estas dos partes dan un modelo conjunto para \(X\) y \(Y\): sabemos que está completamente determinado pues pudimos simular del modelo. Otra manera de entender esto es que cualquier probabilidad que involucra a \(X\) y \(Y\) puede ser calculada con la regla del producto. Aunque no entraremos en detalles, la densidad conjunta de \(X\) y \(Y\) puede definirse en este caso como \[f(x,y) = f_X(x)f_{Y|X}(y|x)\] Sabemos que \(f_X(x) = 1/(15- 3)\) para \(x\) entre 4 y 15 años, y la forma de \(f_{Y|X}(y|x)\) sabemos que es normal con media y varianza conocida (en términos de x). Esta conjunta puede ser integrada sobre cualquier región (al menos en teoría) para calcular la probabilidad de interés.
8.3 Estaturas: variación gamma
Podemos juntar estos bloques de densidades condicionales para construir otro tipo de modelos. Por ejemplo, supondremos que la estatura dada la edad es una distribución gamma \((k,\lambda)\) y la misma media y desviación estándar que vimos arriba. Como la media de una gamma de este tipo es \(\mu = k/\lambda\) y su desviación estándar es \(\sigma = \sqrt{k}/\lambda\), podemos despejar \(k\) y \(lambda\) y hacer:
datos_tbl <-
tibble(edad = edades) %>%
mutate(media = 80 + 5.5*edad, desv_est = 3 * sqrt(edad)) %>%
mutate(k = (media/desv_est)^2, lambda = media / desv_est^2) %>%
# para este ejemplo, simulamos con la distribución normal.
mutate(estatura_cm = rgamma(n(), shape = k, rate = lambda))
ggplot(datos_tbl, aes(x = edad, y = estatura_cm)) +
geom_point() +
geom_quantile(method = "rqss", lambda = 10,
quantiles = c(0.10, 0.5, 0.9))
#> Smoothing formula not specified. Using: y ~ qss(x, lambda = 10)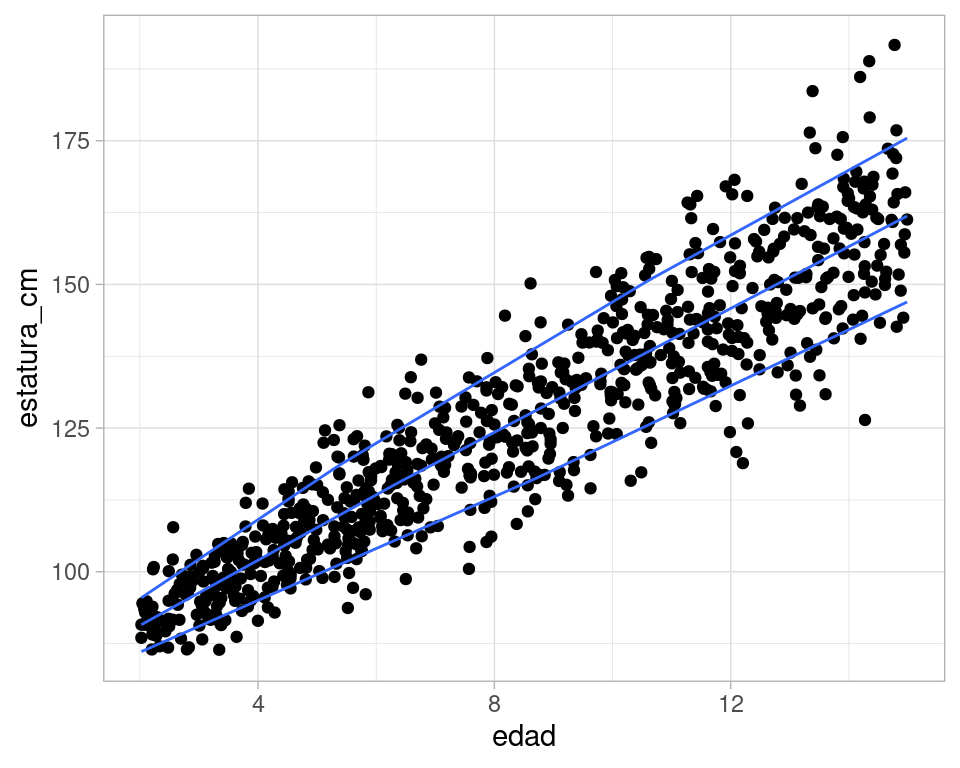
Este modelo es muy similar al normal. Sin embargo, podríamos intentar otras variaciones si cambiamos la magnitud de la desviación estándar en relación a la media, por ejemplo:
datos_tbl <-
tibble(edad = edades) %>%
mutate(media = 30 + 10*edad, desv_est = 7 * (edad)) %>%
mutate(k = (media/desv_est)^2, lambda = media / desv_est^2) %>%
# para este ejemplo, simulamos con la distribución normal.
mutate(medicion_y = rgamma(n(), shape = k, rate = lambda))
ggplot(datos_tbl, aes(x = edad, y = medicion_y)) +
geom_point() +
geom_quantile(method = "rqss", lambda = 10,
quantiles = c(0.10, 0.5, 0.9))
#> Smoothing formula not specified. Using: y ~ qss(x, lambda = 10)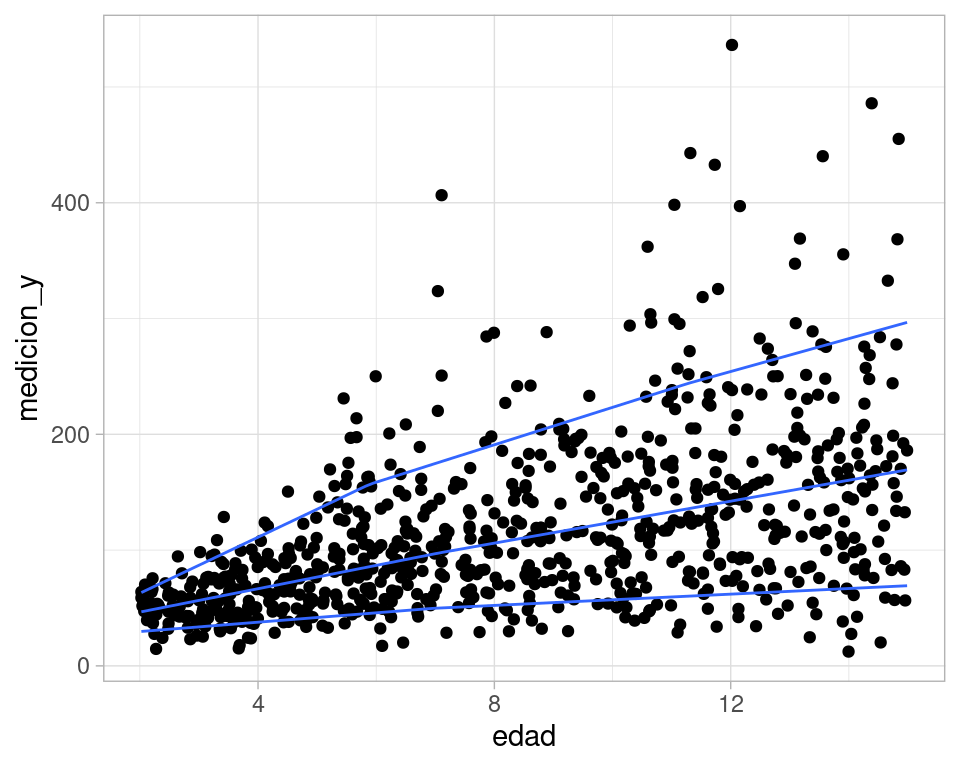
Este caso claramente no serviría para modelar estaturas, pero podemos ver cómo introdujimos asimetría considerable en las distribuciones condicionales de y dado x una vez que especificamos la media y la varianza condicionales. Este tipo de asimetrías no es raro observarla en los datos.
8.4 Ejemplo: cuentas y propinas, versión 1
Para nuestro ejemplo de cuentas de un restaurante, podríamos establecer como modelo inicial:
- La cuenta total \(C\) tiene una distribución gamma \(G(5.4, 0.28)\) (\(k=5.4, \lambda = 0.28\)). La media de cuentas es alrededor de \(k/\lambda \approx 19\) dólares, y la desviación estándar es \(\sqrt{k}/\lambda \approx 8\).
- Dada la cuenta total \(C\), la propina \(P\) es normal con media \(0.15 C\) con desviación estándar \(0.05 C\). Otra manera de ver esto es que la propina se escribe como \(P = C\pi\), donde \(\pi\) es normal con media 0.15 y desviación estándar independiente de \(C\).
Veamos qué datos produce este modelo:
simular_cuentas <- function(n){
cuentas <- rgamma(n, shape = 5.5, rate = 0.22)
propinas <- rnorm(n, 0.15 * cuentas, 0.05 * cuentas)
tibble(rep = 1:n, cuenta_total = cuentas, propina = propinas)
}
set.seed(211)
propinas <- read_csv("datos/propinas.csv")
#>
#> ── Column specification ────────────────────────────────────────────────────────
#> cols(
#> cuenta_total = col_double(),
#> propina = col_double(),
#> fumador = col_character(),
#> dia = col_character(),
#> momento = col_character(),
#> num_personas = col_double()
#> )
cuentas_sim <- simular_cuentas(240) %>%
mutate(tipo = "simulada")
cuentas <- bind_rows(cuentas_sim,
propinas %>% select(cuenta_total, propina) %>% mutate(tipo = "observada"))
ggplot(cuentas %>% filter(tipo == "simulada"),
aes(x = cuenta_total , y = propina)) +
geom_point() +
facet_wrap(~tipo, nrow = 1) +
geom_smooth(se = FALSE, span = 2)
#> `geom_smooth()` using method = 'loess' and formula 'y ~ x'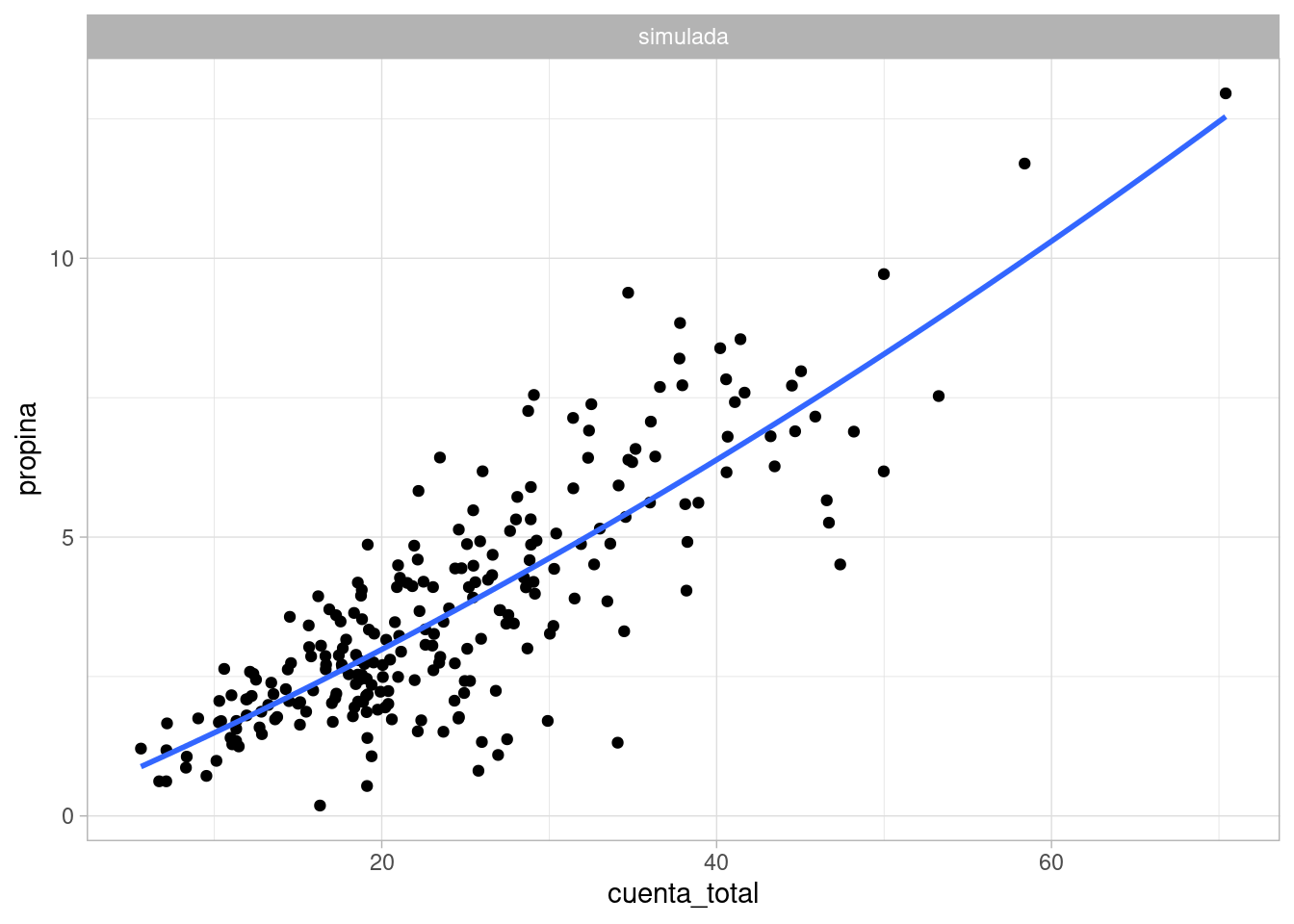
Este modelo puede ser un punto de inicio para modelar los datos observados.
8.5 Modelos conjuntos para factor categórico
Supongamos ahora que la variable \(Y\) es numérica y la variable \(X\) es categórica. En este caso, un modelo conjunto está definido por las probabilidades \(P(X=x)\) junto con densidades condicionales \(Y|X\).
8.5.1 Ejemplo: cuentas y propinas
Supongamos que \(X\) es la hora del día (comida y cena) y que \(Y\) es el tamaño de la cuenta.
Podríamos establecer por ejemplo, que \(Y|X=comida\) es Gamma con media 10 dólares y desviacion estándar 10 dólares. Sin embargo, \(Y|X=cena\) es Gamma con media 25 dólares y desviación estándar 20 dólares. Simulamos y analizamos:
datos_tbl <-
tibble(hora = sample(c("comida", "cena"), 1000, replace = TRUE)) %>%
mutate(media = ifelse(hora == "comida", 10, 25),
desv_est = ifelse(hora == "comida", 10, 20)) %>%
mutate(cuenta = rgamma(n(), shape = (media / desv_est)^2,
rate = media / (desv_est^2)))
ggplot(datos_tbl, aes(x = hora, y = cuenta)) +
geom_boxplot()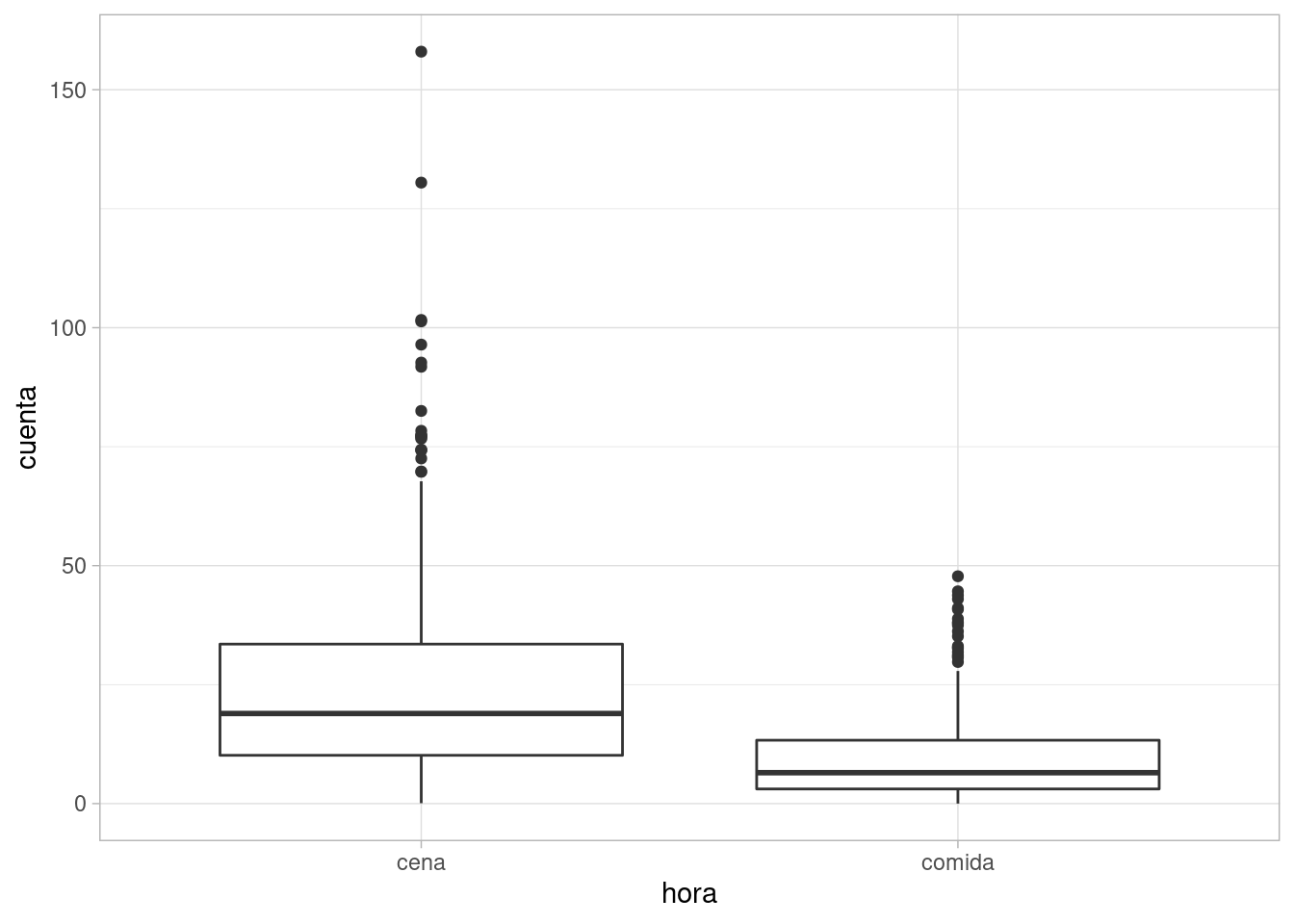
Y esta gráfica busca mostrar una estimación de las distribuciones condicionales de cuenta dado el turno donde el cliente consumió.
8.6 Modelos multivariados
Ahora consideremos que queremos construir un modelo conjunto para tres variables \(X, Y\) y \(Z\). La forma en que procedemos dependerá del problema particular, pero podemos usar la regla del producto como guía. Por ejemplo, podríamos dar una distribución para \(Z\), luego una densidad condicional de \(Y\) dado \(Z\), y finalmente una condicional de \(Y\) dada tanto \(X\) como \(Z\).
library(dagitty)
g <- dagitty('dag {
Z [pos="0,1"]
X [pos="1,0"]
Y [pos="2,1"]
Z -> X -> Y
Z -> Y
}')
plot(g)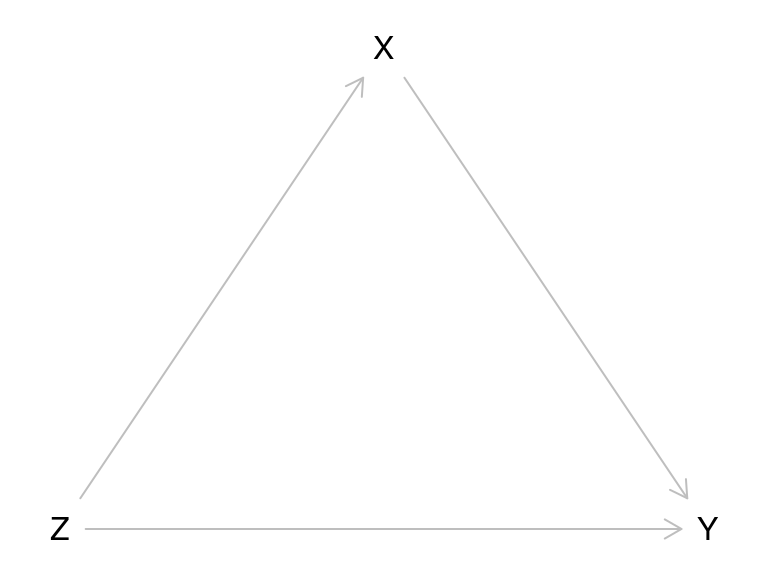 En este caso, cada variable aleatorio es nodo, y representa
una distribución condicional dado sus antecesores. Esta gráfica
por ejemplo, muestra una manera de escribir con la regla del producto
un modelo conjunto, pero podríamos cambiar de posición los nodos
dependiendo de nuestro conocimiento y el problema que queremos resolver.
En este caso, cada variable aleatorio es nodo, y representa
una distribución condicional dado sus antecesores. Esta gráfica
por ejemplo, muestra una manera de escribir con la regla del producto
un modelo conjunto, pero podríamos cambiar de posición los nodos
dependiendo de nuestro conocimiento y el problema que queremos resolver.En algunos casos, es posible simplificar la construcción del modelo eliminando algunas aristas. Supongamos por ejemplo que
- X es la edad de la persona
- Z es “M” of “F”
- Y es su estatura
En este caso, no es necesario especificar la condicional de \(X\) dado \(Z\), pues estas dos son variables independientes. Pondríamos entonces simplemente
library(dagitty)
g <- dagitty('dag {
Z [pos="0,1"]
X [pos="1,0"]
Y [pos="2,1"]
X -> Y
Z -> Y
}')
plot(g)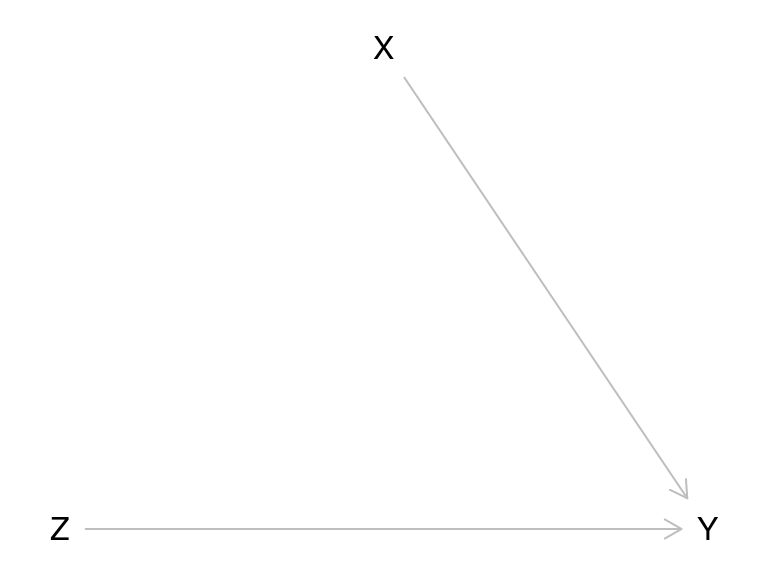 Y solo necesitamos especificar las distribuciones de \(X\), de \(Z\), y la
condicional de \(Y\) dado \(Z\), es decir, la regla del producto se
simplifica a:
Y solo necesitamos especificar las distribuciones de \(X\), de \(Z\), y la
condicional de \(Y\) dado \(Z\), es decir, la regla del producto se
simplifica a:
\[f_{X,Y,Z} = f_Z f_{X|Z} f_{Y|X,Z} = f_Z f_X f_{Y|X,Z}.\]
Siguiendo nuestro ejemplo anterior, consideraremos a
- \(X\) como uniforme en \([4,15]\) (que es nuestro rango de edad de interés)
- \(Z\) es \(M\) con probabilidad 0.5 y \(F\) con probabilidad 0.5
Y podríamos especificar ahora: la condicional de \(Y\) (estatura) es normal con los siguientes parámetros:
- Si \(X\) es la edad y \(Z="F"\), entonces la media es \(70 + 6.5 X\)
- Si \(X\) es la edad y \(Z="M"\), entonces la media es \(80 + 4.5 X\)
- La desviación estándar sólo depende de \(X\), y es igual a \(4\sqrt{X}\).
Simulamos ahora de este modelo probabilístico:
datos_tbl <- tibble(x = runif(1000, 4, 15)) %>%
# independientemente simulamos M o F
mutate(z = sample(c("m", "f"), 1000, replace = TRUE)) %>%
mutate(media = ifelse(z=="f", 70 + 6.5 * x, 80 + 4.5 * x)) %>%
mutate(desv_est = 4 * sqrt(x)) %>%
mutate(estatura = rnorm(n(), media, desv_est))
datos_tbl %>% head(20) %>% kable()| x | z | media | desv_est | estatura |
|---|---|---|---|---|
| 13.042070 | m | 138.6893 | 14.445522 | 135.75933 |
| 11.891004 | f | 147.2915 | 13.793334 | 123.07346 |
| 7.925374 | f | 121.5149 | 11.260816 | 104.36447 |
| 10.208920 | f | 136.3580 | 12.780560 | 129.08575 |
| 9.644507 | m | 123.4003 | 12.422242 | 120.07409 |
| 9.641210 | f | 132.6679 | 12.420119 | 143.88885 |
| 14.231678 | f | 162.5059 | 15.089959 | 143.66741 |
| 4.140385 | f | 96.9125 | 8.139174 | 98.77138 |
| 11.926758 | m | 133.6704 | 13.814056 | 126.91889 |
| 6.071234 | m | 107.3206 | 9.855950 | 126.02192 |
| 9.710636 | f | 133.1191 | 12.464758 | 125.99680 |
| 9.345832 | f | 130.7479 | 12.228381 | 138.87947 |
| 7.522510 | f | 118.8963 | 10.970878 | 124.69338 |
| 12.250602 | m | 135.1277 | 14.000344 | 110.80319 |
| 13.981670 | f | 160.8809 | 14.956829 | 185.22676 |
| 14.338161 | m | 144.5217 | 15.146306 | 124.82693 |
| 7.228936 | m | 112.5302 | 10.754673 | 133.00498 |
| 7.599526 | f | 119.3969 | 11.026896 | 120.01431 |
| 9.753894 | f | 133.4003 | 12.492490 | 131.91527 |
| 9.235258 | m | 121.5587 | 12.155827 | 128.09981 |
Y hacemos algunas gráficas descriptivas:
ggplot(datos_tbl, aes(x = x, y = estatura, colour = z)) +
geom_point()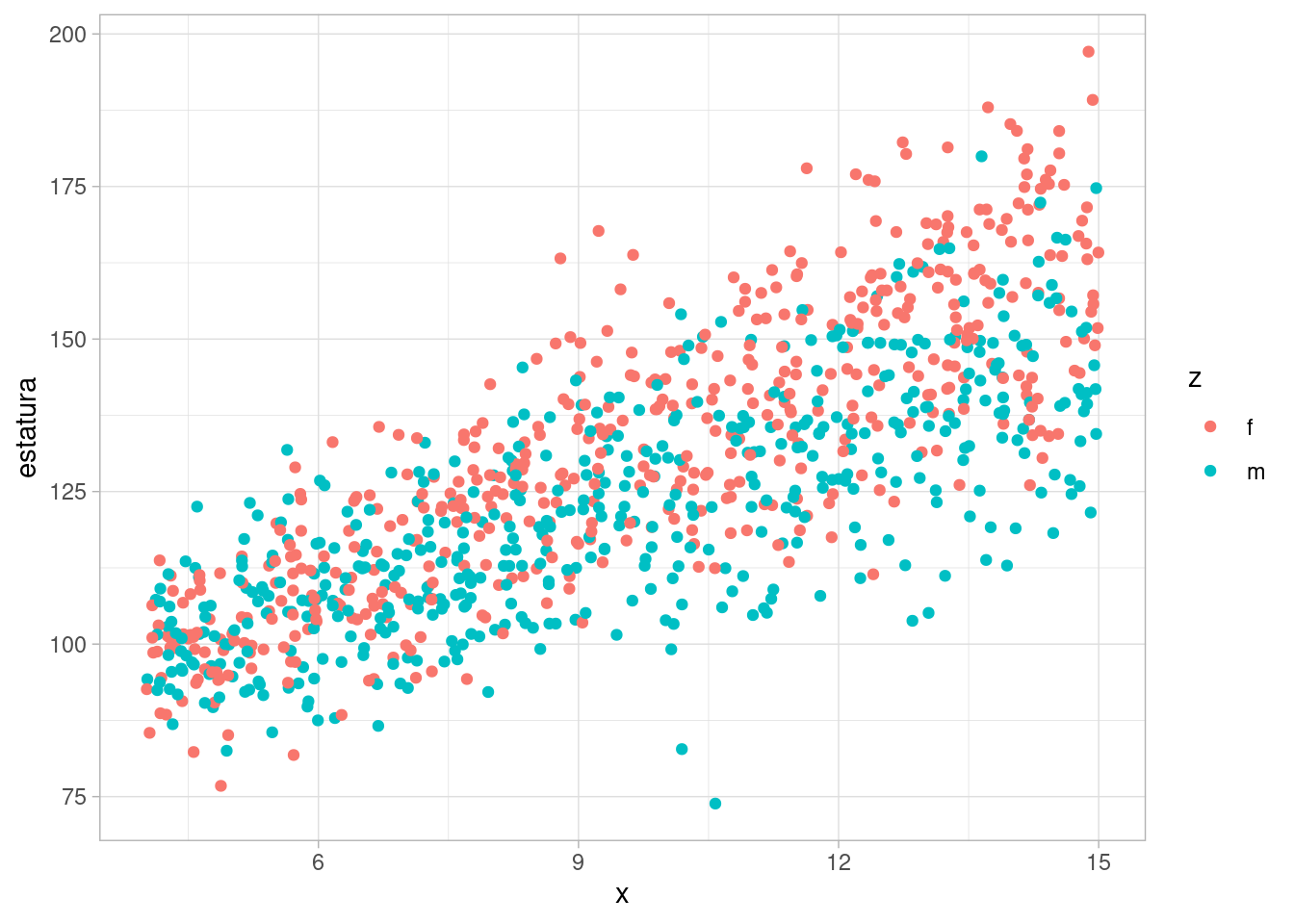
- Discute qué otras cosas podrías cambiar en este modelo probabilístico para que fuera más flexible o más simple. ¿Cómo ajustarías un modelo así a datos reales?
ggplot(datos_tbl, aes(x = x, y = estatura, colour = z)) +
geom_point() +
facet_wrap(~z) +
geom_quantile(method = "rqss", lambda = 10,
quantiles = c(0.10, 0.5, 0.9))
#> Smoothing formula not specified. Using: y ~ qss(x, lambda = 10)
#> Smoothing formula not specified. Using: y ~ qss(x, lambda = 10)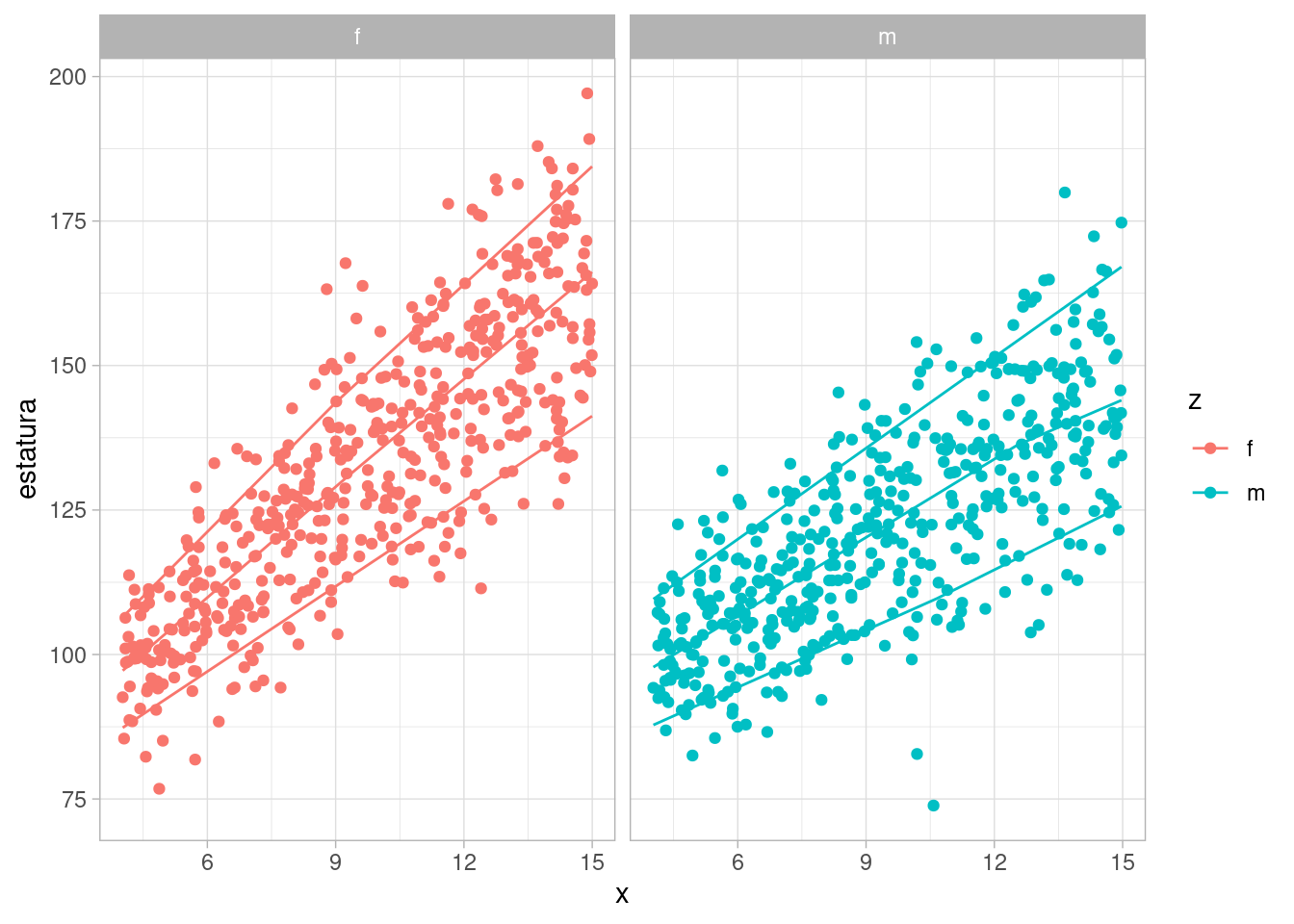
En la modelación probabilística generalmente usamos estos mecanismos (dependencia condicional, independencia) y estos bloques (distribuciones de probabilidad dadas en términos de parámetros) para obtener estimaciones de parámetros de interés.
Las decisiones de cómo usar estos mecanismos y bloques se desprenden de conocimiento de dominio, alcances del análisis, y siempre están sujetos a revisión dependiendo del tipo de desajustes que presenten frente a los datos reales.